Моделирование ХТП
Кинетическое моделирование гетерогенных реакций
Лабораторная работа № 1
Кинетическое моделирование гетерогенных реакций
Часть 1. Система с одной реакцией без изменения количества вещества.
Реакция водяного газа имеет место во многих процессах переработки природного газа, газификации угля и т.п.
CO2 + H2 = CO + H2O
Эта реакция достаточно изучена, известна зависимость константы ее равновесия от температуры.
В [1] исследовался синтез метанола на катализаторе со следующими характеристиками: состав Cu/ZnO/Al2O3, мольное отношение Cu/Zn/Al = 60/30/10, форма — цилиндрические гра-нулы 5 мм диаметром и 5 мм высотой. Было предложено описывать кинетику реакции водяного газа следующим уравнением
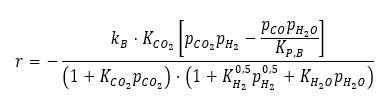
Константа скорости реакции (стадии, определяющей скорость) kB=1,16*1011 exp(-126573/RT)
Константа равновесия реакции KPB=10(-2090/T-2,018)
Константа адсорбции KCO2=1,02*10-6*exp(67439/RT)
Константа адсорбции KH2=2,71*102*exp(-6291/RT)
Константа адсорбции KH2O=3,8*10-10*exp(80876/RT)
1) Начальные мольные доли веществ: водорода — 0,58; CO — 0,06; CO2 — 0,09; вода — 0,27.
2) Давление — 4,5 МПа. Давление остается постоянным.
3) Температура — 220 °С. Температура остается постоянной.
4) Объем — 0,00001 м3.
5) Масса катализатора — 0,0075 кг (из расчета типовой насыпной плотности слоя такого катализатора 750 кг/м3).
Задание:
1. Ознакомьтесь с приближенным (численным) способом решения системы дифференциальных уравнений с использованием метода Эйлера.
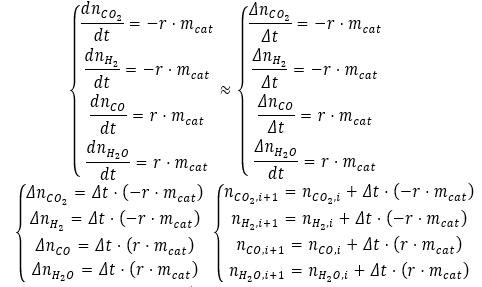
2. С использованием электронных таблиц решите кинетическую модель реакции водяного газа. Выберите как можно меньшее значение шага по времени.
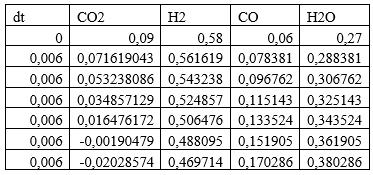
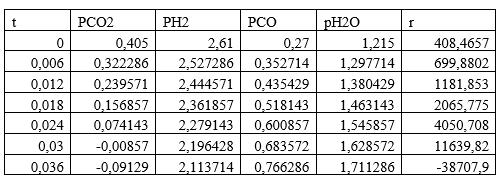
3. Изменяя исходные данные, оцените, в какой момент времени скорость реакции r уменьшается почти до нуля или меняет знак — это соответствует достижению химического равновесия. Какова степень конверсии сырья в этот момент времени? Каков состав смеси?
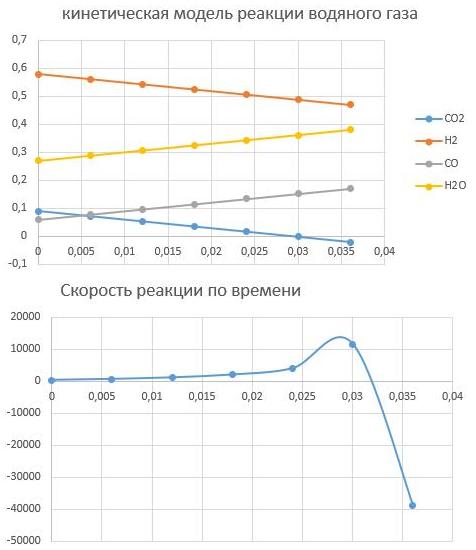
По графикам видно, что скорость останавливается при времени реакции t = 0,032с, при этом равновесный состав Н2 - 0,47; CO — 0,17; CO2 -0; вода — 0,36.Конверсия сырья
αH2=(0,58-0,47)/0,58=0,189=18,9 %
αCO2=(0,09-0)/0,09=1=100%
4. Зная время из п. 3, проведите параметрическое исследование — проварьируйте следу-ющие параметры:
— соотношение CO/CO2 в сырье;
При соотношении CO/CO2 в сырье в начальный момент времени 0,06/0,09 = 0,67
Увеличим CO/CO2 до 0,875, тогда состав станет
Н2 - 0,58; CO — 0,07; CO2 -0,08; вода — 0,27.
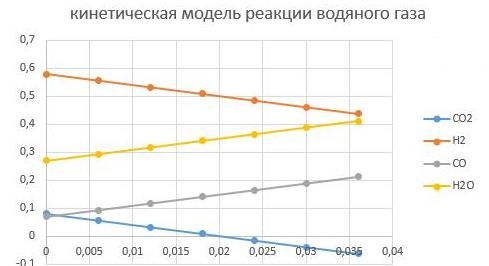
Видно, что так как СО2 стало меньше, то реакции прошла быстрее до полного превраще-ния СО2
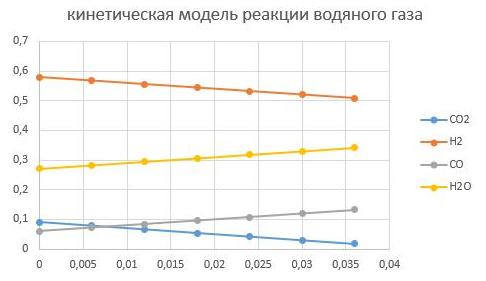
давление Р = 2,5 МПа
давление Р = 6,5 МПа
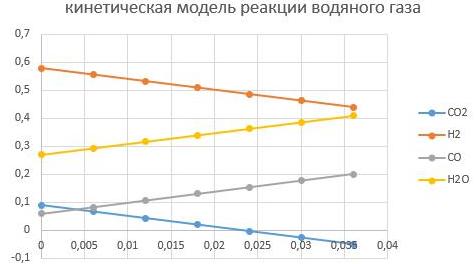
Видно, что увеличение давление способствует интенсифкации реакции
температура в пределах (200–400) °С;
При Т = 200°С
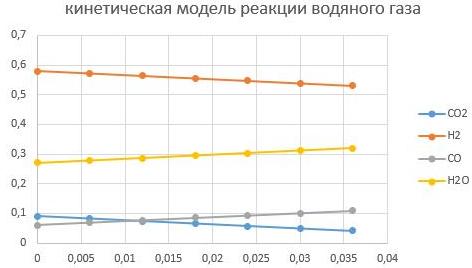
При Т = 400°С
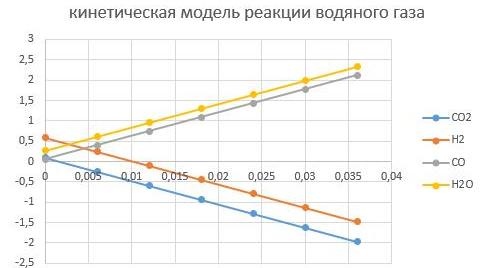
Видно, что увеличение температуры способствует интенсифкации реакции
— масса катализатора в пределах (0,005–0,01) кг.
m_cat=0,005кг
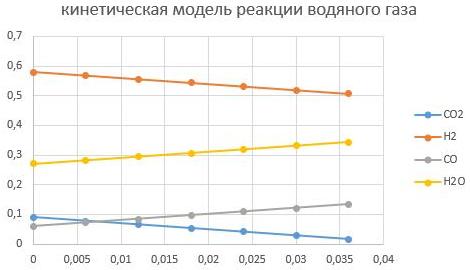
m_cat=0,01кг
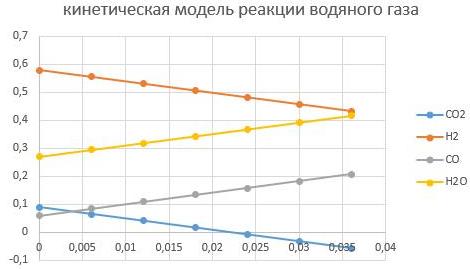
Видно, что увеличение массы катализатора способствует интенсифкации реакции
Часть 2. Система с несколькими реакциями.
Xu и Froment (1989a) [5] предложили для реакций в процессе конверсии водяного пара
СН4 + Н2О = СО + 3Н2 (1)
СО + Н2О = СО2 + Н2 (2)
СН4 + 2Н2О = СО2 + 4Н2 (3)
следующую кинетическую схему:

Используемый 13-ступенчатый механизм показывает конкуренцию за активные центры между метаном и паром.
Выражения для скоростей могут давать немонотонную зависимость скоростей реакций от парциального давления пара и метана.
Кинетическая модель для реакций (1–3) была составлена ими следующим образом:
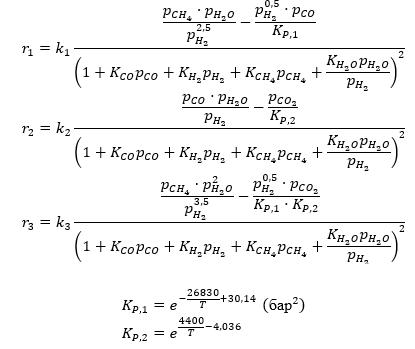
Таблица — Предэкспоненциальные множители для констант скоростей химических реакций, констант адсорбции, энергии активации и теплоты адсорбции
|
Константы |
Предэкспоненциальные множители А |
Энергии активации Ea реакций и теплоты адсорбции Q молекул, кДж/моль |
|
k1, (кмоль бар0,5)/(кг кат-ра ч) |
9,489 · 1015 |
240,10 |
|
k2, кмоль/(кг кат-ра ч бар) |
4,391 · 106 |
67,13 |
|
k3, (кмоль бар0,5)/(кг кат-ра ч) |
2,291 · 1015 |
243,90 |
|
KCO, бар–1 |
8,230 · 10–5 |
70,65 |
|
KCH4, бар–1 |
6,650 · 10–4 |
38,28 |
|
KH2O, бар–1 |
1,770 · 105 |
-88,68 |
|
KH2, бар–1 |
6,120 · 10–9 |
82,90 |
Температурные зависимости констант описываются аррениусовскими уравнениями:
— для констант скоростей ki=Ai⋅exp((-E_(a,i)/RT) )
— для констант адсорбции веществ Ki=Ai⋅exp(Q/RT).
Задание:
1. Повторите графики, полученные в [6, 7] по методу начальных скоростей (Приложение А):
— зависимости скоростей реакций (каждой по отдельности) от парциального давления водяного пара при разных температурах;
— зависимость суммарной скорости превращения метана от парциального давления водяного пара при разных температурах;
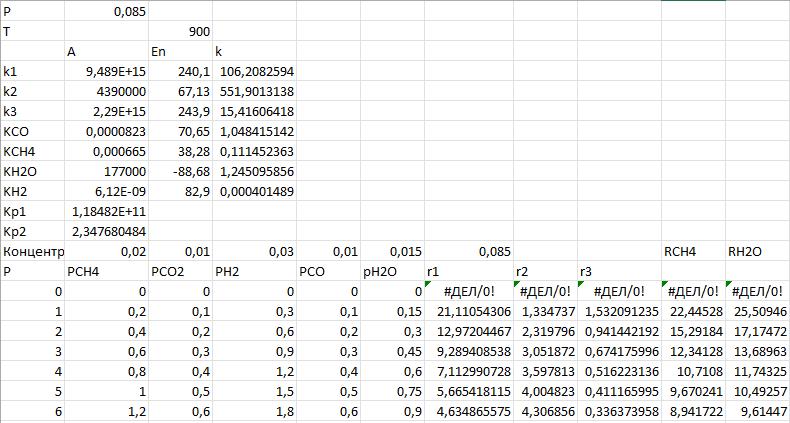
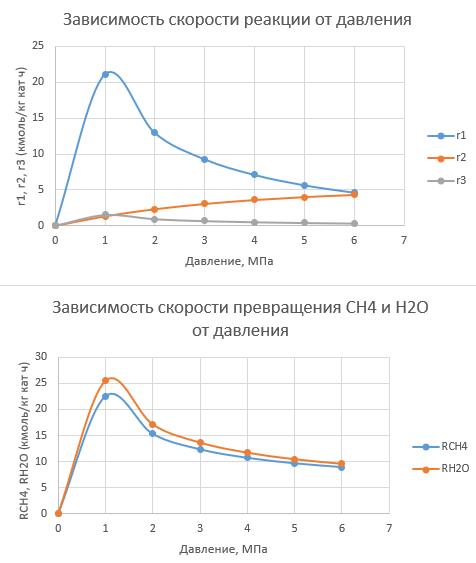
Проанализируйте полученные зависимости. Совпадают ли они с выводами, сделанными при обсуждении данной модели на лекции?
Обратите внимание: исходное парциальное давление пара изменяется, но парциальные давления других компонентов не меняются. Значит, и общее давление должно изменяться, и мольные доли веществ.
Исходные данные используйте из [7]: температуры — 900–1073 К, парциальные давления веществ (кроме водяного пара) — 0,1–0,3 бар.
1. Minji Son, Yesol Woo, Geunjae Kwak, Yun-Jo Lee, Myung-June Park. CFD modeling of a compact reactor for methanol synthesis: Maximizing productivity with increased thermal controllability. International Journal of Heat and Mass Transfer, Volume 145, 2019.
Задачи на моделирование (Термодинамика)
ДЗ1 Расчёт давления пара и точки кипения чистых веществ
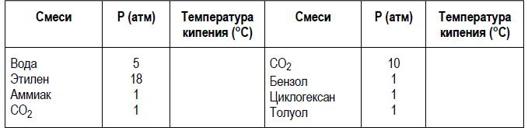
1) Определите абсолютное давление в следующих ёмкостях:
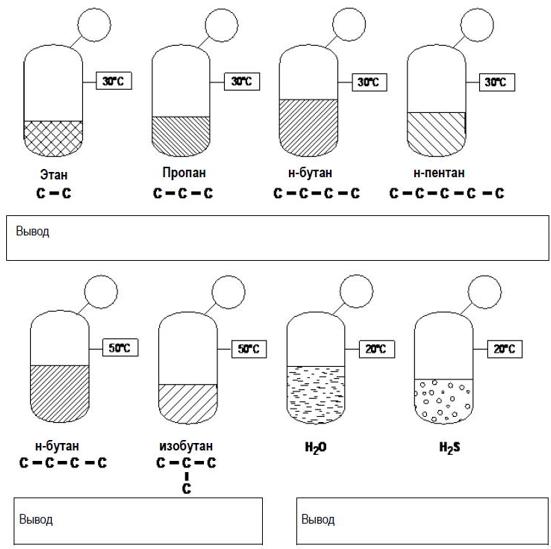
Определите (на основе разных кривых в Справочнике и уравнения Антуана) температуру кипения следующих веществ:
Скачать решение задачи ДЗ1 цена 200р
ДЗ2 Расчёт работы сжатия газа по уравнениям состояния
Имеется резервуар, который содержит 2 моль H2O при 1000 K. Рассчитайте, сколько требуется работы для изотермического и адиабатного сжатия этого газа от объема равного (2 + последняя цифра номера зачётной книжки) л до 1 л,
(а) Используя идеальную газовую модель для воды.
(б) Используя уравнение Редлиха-Квонга
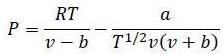
а = 14,24 Дж*К1/2*м3/моль2;
b = 2,11*10-5 м3/моль
Исходный объем V= 2+3 = 5 л
Скачать решение задачи ДЗ2 цена 100р
ДЗ3 Расчёт давления пара смеси углеводородов
Разделение парожидкостной смеси углеводородов F выполняется в сепараторе, как показано ниже:
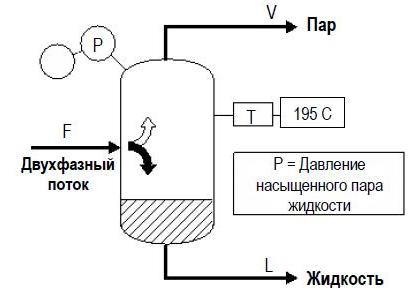
Сырье с расходом F частично испаряется, происходит разделение на две фазы:
– Пар V, выходящий из сепаратора является насыщенным.
– Жидкость L, выходящая из сепаратора является насыщенной. Она находится на уровне точки начала кипения.
Давление в сепараторе представляет собой давление насыщенного пара жидкости L. Для смесей углеводородов оно может быть рассчитано приближенно по закону Рауля, если молекулярный состав жидкости и температура в сепараторе известны, как указано в приведенном ниже примере.
Скачать решение задачи ДЗ3 цена 200р
ДЗ4 Расчёт давления пара смеси углеводородов
Рассчитайте температуру точки начала кипения следующей смеси при абсолютном давлении равном 2 умножить на последнюю цифру номера зачётной книжки) атм, считая парожидкостную систему идеальной.
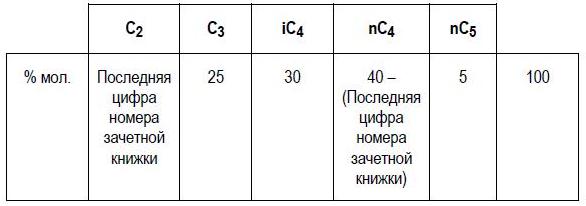
Р = 2·3 = 6 атм
Скачать решение задачи ДЗ4 цена 200р
ДЗ5 Расчёт фазовой диаграммы бинарной смеси углеводородов
– Рассчитайте и нарисуйте (на 2 странице) изобарическую диаграмму равновесия для двухкомпонентной смеси изобутана и н-бутана при абсолютном давлении 5 атм (используйте значения коэффициента фазового равновесия Шейбеля и Дженни из номограммы на 3 странице). Все расчёты приведите на отдельной странице.
– Сделайте вывод о разделении iC4-nC4?
По диаграмме Шейбеля и Дженни
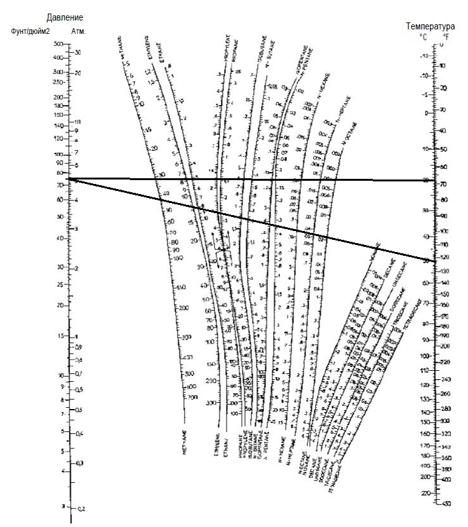
Скачать решение задачи ДЗ5 цена 200р
ДЗ6 Расчёт сепаратора
A - РАСЧЕТ ПО ФРАКЦИЯМ
Установка, показанная ниже, предназначена для сжатия, а затем охлаждения нефтезаводского газа для извлечения СНГ (C3 и C4) в жидкой фазе.
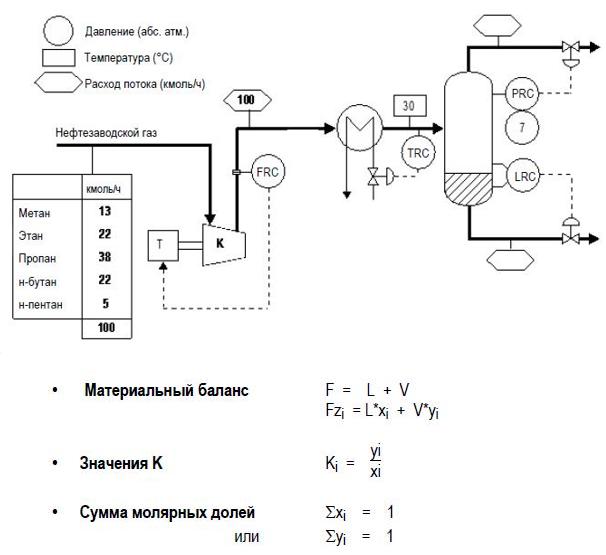
А) Рассчитайте степень извлечения СНГ. Всё расчёты по пункту А привести на отдельной странице.
Б) Расход бензиновой фракции (чистого н-гептана) равен 10 умножить на последнюю цифру номера зачётной книжки.
В) Рассчитайте степень извлечения СНГ. Сравните со случаем А. Всё расчёты по пункту Б и вывод по заданиям А и Б привести на отдельной странице.
Скачать решение задачи ДЗ6 цена 200р
ДЗ7 Расчёт условий появления азеотропа в смеси двух веществ
Имеется смесь 1-пропанола (а) с водой (b). Используя двухпараметрическую модель Маргулеса с указанными параметрами
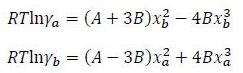
А = 4640 Дж/моль
В = -1700 Дж/моль
определите формирует ли данная смесь азеотроп при температуре (10 + 2*(последняя цифра номера зачётной книжки)) оС. Если да, то при каком давлении появляется азеотроп?
T = 10+2*3 = 16ºC
Скачать решение задачи ДЗ7 цена 200р
Математическое моделирование химико-технологических процессов
Задача 1.1 В таблице 1.1 приведены данные разгонки широкой бензиново фракции. Постройте серию эмпирических моделей в виде алгебраических степенных полиномов от первой до 5 степени. Оцените адекватность каждой модели, рассчитав коэффициент детерминации, остаточную сумму.
Таблица 1.1 (начало)
|
Доля отгона, % |
2,84 |
6,19 |
10,22 |
15,09 |
20,82 |
27,15 |
33,68 |
40,10 |
46,36 |
52,53 |
|
ТНК, оС |
0.2 |
11.4 |
22.6 |
33.8 |
44.9 |
56.1 |
67.3 |
78.5 |
89.7 |
100.8 |
Таблица 1.1 (продолжение)
|
Доля отгона, % |
58,69 |
64,89 |
71,09 |
77,07 |
82,53 |
87,25 |
91,25 |
94,63 |
97,51 |
|
ТНК, оС |
112 |
123.2 |
134.4 |
145.6 |
156.7 |
167.9 |
179.1 |
190.3 |
201.5 |
Скачать задачу 1.1 (моделирование процессов) цена 100р
Задача 1.2 По приведенным в Таблице 1.2 данным зависимости плотности указанных жидкостей от температуры построить эмпирическую модель и оценить её адекватность. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.2 - Плотность в кг/м3 при указанной температуре в ºС
|
Вар |
Вещество |
-20 |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
0 |
Ацетон |
835 |
813 |
791 |
768 |
746 |
719 |
693 |
665 |
Скачать задачу 1.2 (моделирование процессов) цена 100р
Задача 1.3 В Таблице 1.3 приведены зависимости вязкости жидкости от температуры для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.3 - Динамическая вязкость в мПа*с при указанной температуре в ºС
|
Вещ-во |
Динамическая вязкость в мПа*с при указанной температуре в °С |
|||||||||||
|
-20 |
-10 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
120 |
|
|
Ацетон |
0,5 |
0,442 |
0,395 |
0,356 |
0,322 |
0,293 |
0,268 |
0,246 |
0,23 |
0,2 |
0,17 |
0,15 |
Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков.
Скачать задачу 1.3 (моделирование процессов) цена 100р
Задача 1.4 В Таблице 1.4 приведены зависимости удельной теплоты парообразования (в кДж/кг) от температуры (в оС) для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.4 - Теплота парообразования кДж/кг от температуры в ºС
|
Вар |
Вещ-во |
0 |
20 |
60 |
100 |
140 |
|
0 |
Ацетон |
566 |
553 |
520 |
474 |
- |
Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков.
Скачать задачу 1.4 (моделирование процессов) цена 100р
Задача 1.5 Зависимость константы скорости реакции от температуры для ряда веществ приведена в Таблице 1.5. Рассмотрите возможность описания этой зависимости уравнением Аррениуса. По приведенным данным определите константы уравнения Аррениуса – энергию активации и предэкспоненциальный фактор. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.5 - Константа скорости реакции в с-1 от температуры в ºС
|
Вар |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
|
0 |
0,05 |
0,25 |
0,6 |
0,98 |
1,35 |
1,99 |
2,87 |
4,56 |
8,43 |
Скачать задачу 1.5 (моделирование процессов) цена 100р
Задача 1.6. В таблице 1.6. приведена зависимость теплоемкости газов от температуры для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
|
Вар |
Вещество |
Теплоемкость в кДж/кг*К от температуры в К |
|||||||
|
273 |
300 |
500 |
700 |
900 |
1100 |
1300 |
1500 |
||
|
0 |
О2 |
0,9148 |
0,9169 |
0,9391 |
0,9688 |
0,996 |
1,0182 |
1,0371 |
1,053 |
Скачать задачу 1.6 (моделирование процессов) цена 100р
2 Физические свойства чистых веществ – уравнения состояния
Задача 2.1 Найти удельный объем н-бутана при температуре 393.3 К и давлении 16.6 атм, используя уравнение состояния Рейндлиха-Квонга. Молекула н-бутана имеет симметричное строение, поэтому уравнение Рейндлиха-Квонга должно дать результат, близкий к экспериментальному (уравнения Соаве-Рейндлиха-Квонга и Пенга-Робинсона использовать необязательно). Так как давление выше 10 атм, можно ожидать существенных отклонений от закона идеального газа. Критические параметры бутана: Tc = 425.2 K, Pc = 37.5 атм.
Скачать задачу 2.1 (моделирование процессов) цена 100р
Задача 2.2 Определите молярный объем аммиака при давлении 56 атм и температуре 450 К, используя уравнение Рейндлиха-Квонга. Критические показатели для аммиака TС = 405.5 К, РС = 111.3 атм, a = 4.2527, b = 0.02590. Единицы измерения a и b соответствуют v, измеряемому в л/(г моль).
Скачать задачу 2.2 (моделирование процессов) цена 100р
Задача 2.3 Решите задачу №2.2, используя уравнения Соаве-Рейндлиха-Квонга и Пенга- Робинсона. Ацентрический фактор для молекулы аммиака принять равным 0.25. Объясните различия.
Скачать задачу 2.3 (моделирование процессов) цена 100р
Задача 2.4 Имеется смесь, состоящая из 25% аммиака, а оставшиеся азот и водород находятся в мольном соотношении 1:3. Газ находится при давлении 270 атм и температуре 550 К. Рассчитайте мольный объем смеси, используя уравнения идеального газа, Рейндлиха-Квонга и Соаве-Рейндлиха-Квонга. Сравните результаты. Объясните различия. Является ли газ идеальным?
Скачать задачу 2.4 (моделирование процессов) цена 100р
Задача 2.5 Определите молярный объем метанола при давлении 100 атм и температуре 300 °С, используя уравнение Соаве-Рейндлиха-Квонга. Критические показатели для метанола TС = 512.6 К, РС = 79.9 атм, a = 8.96, b = 0.04561, ω = 0.559. Единицы измерения a и b соответствуют v, измеряемому в л/(г моль). Объясните почему в данном случае не подходят уравнения идеального газа и Рейндлиха-Квонга. Дополнительные сведения: при давлении 9.174 МПа и температуре 300 °С мольный объем метанола составляет 0.373 л/(г моль).
Скачать задачу 2.5 (моделирование процессов) цена 100р
Задача 2.6 Имеется смесь на выходе из реактора для синтеза метанола: СО – 100, Н2 – 200, метанол – 100 кмоль/ч. Газ находится при давлении 100 атм и температуре 300 °С. Рассчитайте мольный объем смеси, используя уравнения идеального газа, Рейндлиха-Квонга и Соаве-Рейндлиха-Квонга. Объясните различие результатов. Почему уравнения идеального газа и РК дают неверные результаты. Ацентрические факторы: СО – 0.049, Н2 – 0.22, метанол – 0.559.
Скачать задачу 2.6 (моделирование процессов) цена 100р
3 Равновесие «пар-жидкость»
Задача №3.1. Провести расчёт сепарационного блока (на рисунке) процесса разделения многокомпонентной углеводородной смеси (рассчитать состав и количество газовых и жидких потоков на выходе из каждого сепаратора) и исследовать влияние технологических параметров на процесс сепарации.
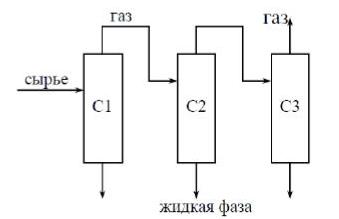
Рис. 3.1 - Принципиальная схема сепарационного блока. С – это сепараторы.
Таблица 3.1. Исходные данные для расчета процесса сепарации
|
Компонент |
Мольная масса |
Мол масса |
Плотность газа, кг/м3 |
Плотность жидкости, кг/м3 |
Темп. кипения, ºС |
Критическая темп-ра, К |
Критическое давление, атм |
|
CO2 |
0,00538 |
4 |
1,9650 |
859 |
-78,2 |
304,2 |
72,83 |
|
N2 |
0,02648 |
28 |
1,2510 |
570 |
-195,8 |
126,2 |
33,5 |
|
CH4 |
0,8486 |
16 |
0,7162 |
300 |
-161,58 |
190,6 |
45,4 |
|
C2H6 |
0,0424 |
30 |
0,3420 |
460 |
-88,7 |
305,4 |
48,2 |
|
C3H8 |
0,2628 |
44 |
1,969 |
501 |
-42,06 |
369,8 |
41,9 |
|
i-C4 |
0,00759 |
58 |
2,5948 |
557 |
-11,73 |
408,1 |
36 |
|
C4 |
0,00548 |
58 |
2,5948 |
580 |
-0,5 |
425,9 |
37,5 |
|
C5 |
0,0083 |
72 |
3,22 |
616 |
36,1 |
469,6 |
33,3 |
|
Остаток |
0,02692 |
108 |
3,88 |
721 |
100,7 |
537,3 |
28 |
|
H2O |
0,00358 |
18 |
0,804 |
1000 |
100 |
647,3 |
217,6 |
|
CH3OH |
0,00085 |
32 |
2,678 |
791 |
64,65 |
512,6 |
79,9 |
Базовые термобарические условия в сепараторах:
P1 = 13,8 МПа, Т1 = 21.8 ºС (сепаратор С1);
P2 = 9,7 МПа, Т2 = 8.6 ºС (сепаратор С2);
P3 = 5,4 МПа, Т3 = 34.8 ºС (сепаратор С3).
После выполнения базового расчёта необходимо исследовать влияние технологических параметров на процесс сепарации согласно своему варианту. Вариант выбирается по последнему числу номера зачётной книжки.
Вариант 0 Исследовать влияние температуры в первом сепараторе
Скачать задачу 3.1 (моделирование процессов) цена 200р
4 Гидродинамические модели
Задача 4.1 (вар 8) Через насадочный аппарат длиной L = 10 м, внутренним диаметром d = 0,065 м и коэффициентом заполнения насадкой ϕ=0,67 протекает жидкость с объемной скоростью v = 0,001 м3/с. Построить математическую модель структуры гидродинамического потока в аппарате.
|
t, c |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
c |
0 |
0,1 |
1,1 |
3,6 |
7,2 |
11,3 |
14,9 |
17,6 |
19,1 |
19,5 |
продолжение таблицы
|
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
29 |
30 |
|
19 |
16 |
12,1 |
8,4 |
5,4 |
3,4 |
2 |
1,2 |
0,6 |
0,8 |
0,5 |
Скачать задачу 4.1 (моделирование процессов) цена 200р
Задача 4.2 Построить ячеечную модель гидродинамики насадочного абсорбера по газовому потоку. Высота насадки 11.5 м, площадь поперечного сечения абсорбционной колонны 1.8 м2, объемная скорость потока 10 000 м3/ч.
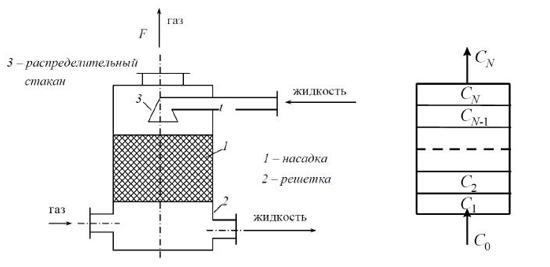
Рис. 4.2. Насадочный абсорбер и его ячеечная схема.
Начальная концентрация абсорбируемого компонента в газовом потоке и экспериментальная кривая абсорбции (зависимость концентрации компонента на выходе из колонны от времени) приведены в таблице 4.2. Вариант выбирается по последнему числу номера зачётной книжки. Необходимо выполнить расчёты при разных значениях числа ячеек ячеечной модели и выбрать оптимальное число ячеек. Сделать вывод.
Начальная концентрация абсорбируемого компонента в % (об.) 0,155
|
Время, с |
вар 0 |
|
0 |
0 |
|
1 |
0,0025 |
|
2 |
0,01 |
|
3 |
0,026 |
|
4 |
0,049 |
|
5 |
0,072 |
|
6 |
0,09 |
|
7 |
0,115 |
|
8 |
0,13 |
|
9 |
0,146 |
|
10 |
0,154 |
Скачать задачу 4.2 (моделирование процессов) цена 200р
Задача 5.1 В теплообменнике типа «труба в трубе» охлаждается жидкость. Хладоагент и охлаждающаяся жидкость движутся прямотоком. Построить математическую модель теплообменного аппарата. Определить температуру теплоносителей на выходе из аппарата. Построить температурные профили по длине аппарата. Исходные данные приведены в таблице 5.1.
Таблица 5.1 – Исходные данные
|
Вариант |
Теплоноситель |
Начальная температура, ºС |
Объёмный расход, м3/с |
Плотность, кг/м3 |
Теплоёмкость, Дж/кг ºС
|
|
10 |
Горячий Холодный |
220 35 |
2,4*10-4 5,5*10-4 |
900 990 |
3.53*103 4.0*103 |
Исследования по длине теплообменника проводятся с целью определения длины, необходимой для завершения процесса теплообмена. Длину теплообменника увеличивают до тех пор, пока процесс теплообмена практически не завершится, т. е. пока разность температур горячего теплоносителя и хладоагента не достигнет 1.5–2 ºС.
Дополнительно нужно исследовать влияние температуры и расхода теплоносителя и хладоагента. Исследования по изменению температуры проводятся с целью изучения влияния температуры хладоагента на расход хладоагента. После изменения температуры хладоагента изменяют расход хладоагента до тех пор, пока конечные температуры горячего теплоносителя и хладоагента не достигнут требуемых значений.
Скачать задачу 5.1 (моделирование процессов) цена 200р
Основные понятия по моделированию
В соответствии с классификацией основных процессов химической технологии по способу создания движущей силы процесса выделяют следующие группы процессов: гидромеханические, тепловые, массообменные, механические и химические.
Химико-технологический процесс складывается из совокупности физических и химических явлений. Основные стадии процесса:
-подвод исходных реагентов в зону реакции (совершается путем молекулярной диффузии, конвекции, абсорбции, десорбции, конденсации, испарения и т.п.)
-химические реакции (в системах обычно протекают несколько последовательных или параллельных реакций, приводящих к образованию целевых (основных) и побочных продуктов реакции); расчеты химико-технологических процессов проводятся обычно с учетом основных реакций, определяющих количество и качество получаемых целевых продуктов;
-отвод продуктов реакций из зоны реакции (осуществляется также как и подвод реагентов за счет диффузии, конвекции или путем перехода вещества из одной фазы в другую).
Скорость протекания каждой стадии технологического процесса может лимитировать общую скорость процесса.
Если общая скорость лимитируется скоростью протекания химической реакции, то процесс протекает в кинетической области; скорость процесса в этом случае можно повысить, изменяя температуру протекания процесса, концентрации исходных реагентов, или использую катализаторы – вещества ускоряющие протекание химических реакции.
Если скорость процесса лимитирует подвод или отвод реагентов, то процесс проходит в диффузионной области. Скорость таких процессов можно повысить за счет турбулизации потоков, прибегая к перемешиванию, повышая температуру или концентрацию.
Классификация химических процессов и реакторов
Химические реакции, составляющие основу ХТП, подразделяются по сложности: на простые и сложные (последовательные и параллельные); по типу взаимодействия реагентов: на гомолитические (окислительно-восстановительные) и гетеролитические (кислотно-основные); по тепловому эффекту: экзо- и эндотермические (с выделением и поглощением тепла соответственно) и др.
Химико-технологические процессы классифицируют по целому ряду признаков: по наличию катализатора, по фазовому состоянию реагентов и катализаторов, по характеру протекания процесса, по гидродинамическим признакам по температурному режиму и др.
Реакционные аппараты, предназначенные для осуществления химических процессов, принято подразделять по следующим признакам: по характеру действия, по гидродинамическим режимам в аппарате; по термодинамическим признакам; по фазовому состоянию регентов и катализаторов; по состоянию катализатора; по давлению и др. Рассмотрим некоторые классификационные признаки.
-По наличию катализатора выделяют каталитические и некаталитические. Первые из них протекают в присутствии катализаторов – веществ, ускоряющих химические превращения, что позволяет проводить процессы в более мягких условиях (снизить температуру), повысить выход целевого продукта и т.п. Некаталитические процессы протекают, как правило, при высоких температурах.
-По фазовому состоянию процессы подразделяются на гомогенные (когда все веществ находятся в одной фазе) и гетерогенные (две и более фаз – Г-Ж, Г-Т, Ж-Т; в эту группу входят и гомогенные реакции, протекающие на границе раздела фаз, например реакции на твердом катализаторе)
-По характеру протекания процесса во времени различают процессы периодические и непрерывные. (см. классификацию по ПАХТ)
-По гидродинамическому режиму различают два предельных случая перемешивания реагентов и продуктов реакции: полное смешение и идеальное вытеснение; на практике в аппаратах не реализуются идеальные режимы и имеет место режим, близкий к одному из них и занимающий промежуточное место между ними - режим частичного перемешивания. Если рассмотреть реакторы (рис.1) с учетом данной классификации, то можно отметить следующие их конструкционные особенности. Реакторы полного (или частичного смешения) представляют собой аппараты с перемешивающими устройствами (мешалками) кубового (емкостного) типа, когда диаметр и длина (высота) аппарата соизмеримы. Аппараты полного вытеснения (последующие слои вытесняют предыдущие без продольного перемешивания) представляют собой трубчатые реакторы большой длины и малого диаметра (змеевик).
-Тепловой эффект. Любая химическая реакция сопровождается выделением или поглощением тепла и в соответствии с первым законом термодинамики тепловой эффект реакции (Q) равен изменению внутренней энергии системы (ΔU) и работы (А), совершаемой системой при изменении ее объема в результате протекания реакции (расширение или сжатие), а при постоянном объеме определяется только первым параметром. По тепловому эффекту выделяют реакции, идущие с выделением тепла (экзотермические) или с поглощением тепла (эндотермические). Тепловой эффект реакции зависит от агрегатного состояния исходных веществ и продуктов реакции, а также от температуры. В случае изменения агрегатного состояния при расчете теплового эффекта учитывают теплоту фазового перехода (теплота испарения, конденсации, плавления, затвердевания). Тепловой эффект реакций определяют экспериментально или вычисляют, используя закон Гесса (следствие первого закона термодинамики), согласно которому тепловой эффект химической реакции простых веществ зависит от исходного и конечного состояния системы и не зависит от пути по которому протекает реакция. Определяют его как разность сумм теплот образования продуктов реакции и исходных веществ:
(1)
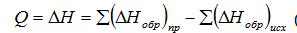
или как разность сумм теплот сгорания исходных веществ и продуктов реакции. При расчетах используют теплоты образования и сгорания для стандартного состояния веществ, найденные в справочной литературе. Суммарный тепловой эффект химического процесса, описываемого несколькими химическими реакциями, определяется с учетом этого параметра для каждой реакции и зависит от глубины превращения.
С учетом общего теплового эффекта процесса определяется его температурный режим, технологическая схема и конструкция реактора.
- По температурному режиму (по термодинамическим признакам) реакторы и протекающие в них процессы подразделяют на изотермические, адиабатические и политротические (программно-регулируемые).
В изотермических реакторах температура постоянна во всем реакционном объеме (в любой части аппарата) за счет отвода или равномерного распределения тепла для экзотермических реакций или за счет подвода тепла для эндотермических процессов (за счет равномерного подвода или отвода тепла в зависимости от знака теплового эффекта реакции). Идеальный изотермический режим реализуется только в аппаратах полного смешения.
В адиабатических реакторах процесс протекает без теплообмена с внешней средой (без подвода или отвода тепла). При этом температуры исходных веществ и продуктов реакции будут отличаться с учетом знака теплового эффекта (для экзотермических – выше температура продуктов реакции; для эндотермических – выше температура исходных веществ). Идеальный адиабатический режим возможен только в аппаратах идеального вытеснения при полной изоляции от внешней среды.
В политропических реакторах для предотвращения значительного перепада температур в аппарате обеспечивается теплообмен реактора с внешней средой т.е. осуществляется либо подвод тепла в зону реакции (для эндотермических процессов), либо отвод тепла (для экзотермических). Промышленные реакторы имеют в большинстве своем политропический температурный режим. Теплообмен с внешней средой в таких процессах может осуществляться непрерывно или ступенчато. В первом случае поверхность теплообмена размещена непосредственно в зоне реакции; во втором – вне зоны реакции в специальных межсекционных устройствах. Для организации теплообмена используют чаще всего различного рода теплообменные устройства (встроенные или выносные теплообменники), приведенные на рис. 2.
-Для гетерогенных процессов в зависимости от направления потоков реагентов или катализаторов различают прямоточные, противоточные или ступенчато-противоточные реакторы (в последнем случае катализатор последовательно перемещается от одной ступени к другой в противотоке с исходным сырьем). Данная классификация необходима для определения характера изменения движущей силы процесса по высоте (длине) аппарата.
-Для процессов, протекающих в газовой фазе характерны повышенные давления. В этой связи предусмотрено деление реакторов по давлению на аппараты низкого (до 10 МПа), высокого (до 100 МПа) и сверхвысокого давления. С учетом давления определяется и конструктивное оформление аппарата.
-По назначению предусмотрено деление аппаратов с учетом процесса, протекающего в них, например реактор каталитического крекинга, реактор риформинга, реактор алкилирования и т.д.
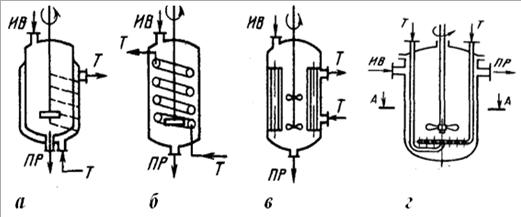
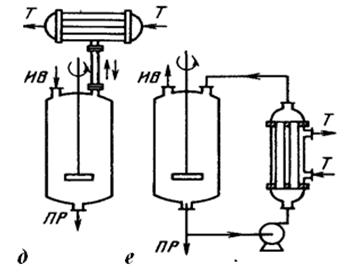
Рис. 2. Схемы теплообменных устройств реакторов:
а – наружная рубашка;
б - встроенный внутренний змеевик;
в - встроенный теплообменник из прямых труб;
г – встроенный спиральный элемент;
д - выносной конденсатор;
е - выносной теплообменник,
Потоки: ИВ - исходные вещества; ПР - продукты реакции; Т - теплоноситель
Решение задач по моделированию от 100руб
Меделирование химико-технологических процессов
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ КИНО И ТЕЛЕВИДЕНИЯ
Кафедра технологии полимеров и композитов
ТЕМЫ КУРСОВЫХ РАБОТ
1. Методы анализа поведения химико-технологических систем. Предварительная обработка информации.
2. Методы анализа поведения химико-технологических систем. Корреляционный анализ.
3. Методы анализа поведения химико-технологических систем. Дискриминантный анализ.
4. Планирование эксперимента в химии и химической технологии. Построение математических моделей на основе полного факторного эксперимента.
5. Планирование эксперимента в химии и химической технологии. Построение математических моделей на основе дробного факторного эксперимента.
6. Методы анализа поведения химико-технологических систем. Системный анализ.
7. Методы анализа поведения химико-технологических систем. Регрессионный анализ.
8. Методы анализа поведения химико-технологических систем. Кластерный анализ.
9. Методы анализа поведения химико-технологических систем. Дисперсионный анализ.
10. Методы анализа поведения химико-технологических систем. Оценка однородности и воспроизводимости информации.
11. Изучение кинетики реакции коксования из нефтяного сырья (гудрон 1) методами математического моделирования.
12. Изучение кинетики коксования из нефтяного сырья (гудрон 2) методами математического моделирования.
13. Изучение кинетики реакции коксования из нефтяного сырья (ближневосточная нефть) методами математического моделирования.
14. Изучение кинетики реакции коксования из нефтяного сырья (тяжелый газойль каталитического крекинга) методами математического моделирования.
15. Изучение кинетики пиролиза пропана методами математического моделирования.
16. Изучение кинетики реакции алкилирования бензола пропиленом методами математического моделирования.
17. Изучение кинетики реакции каталитического окисления пропилена методом математического моделирования.
18. Изучение кинетики реакции каталитического окисления бензола в малеиновый ангидрид методами математического моделирования.
19. Изучение кинетики реакции термического разложения этана методами математического моделирования.
20. Изучение кинетики реакции термического разложения метана методами математического моделирования.
21. Изучение кинетики реакции каталитического окисление о-ксилола методами математического моделирования.
22. Изучение кинетики реакции окислительного аммонолиза о-ксилола методами математического моделирования.
23. Изучение кинетики окисления н-бутена методами математического моделирования.
24. Изучение кинетики реакции жидкофазного каталитического окисления нафталина методом математического моделирования.
25. Изучение кинетики реакции жидкофазного каталитического окисления п-ксилола методом математического моделирования.
26. Изучение кинетики реакции полимеризации этилена при средних давлениях с инициатором.
27. Изучение кинетики реакции полимеризации этилена при средних давлениях на твердых катализаторах.
28. Изучение кинетики реакции инициированного окисления полиэтилена.
29 Изучение кинетики реакции инициированного окисления полипропилена.
30. Изучение кинетики реакции инициированного окисления сополимера пропилена с этиленом.
Выполнение курсовых проектов от 500руб


