Решения задач по Рабиновичу 101-300
Задача 102 (Рабинович). Найти среднюю теплоемкость с'рт и c'vm для воздуха в пределах 400—1200 °С, считая зависимость теплоемкости от температуры нелинейной.
Ответ: с’pm = 1,4846 кДж/(м3. К), с’vm = 1,1137 кДж/(м3. К).
Скачать решение задачи 102 (Рабинович) цена 50р
Задача 103 (Рабинович). Найти среднюю теплоемкость срт и с’pт углекислого газа в пределах 400 - 1000 °С, считая зависимость теплоемкости от температуры нелинейной.
Отв. срт = 1,2142 кДж/(кг . К); с’pт = 2,3865 кДж/(м3. К).
Скачать решение задачи 103 (Рабинович) цена 50р
Задача 104 (Рабинович). Определить среднюю массовую теплоемкость при постоянном объеме для азота в пределах 200 - 800 °С, считая зависимость теплоемкости от температуры нелинейной.
Oтвет: cvm= 0,8185 кДж/(кг . К).
Скачать решение задачи 104 (Рабинович) цена 50р
Задача 106 (Рабинович). Воздух в количестве 6 м3 при давлении р1 = 0,3 МПа и температуре t1 — 25 0С нагревается при постоянном давлении до t2 — 130 °С. Определить количество подведенной к воздуху теплоты, считая с = const.
Ответ: Qp≈2231 кДж
Скачать решение задачи 106 (Рабинович) цена 50р
Задача 107 (Рабинович). Опытным путем найдены следующие значения истинной мольной теплоемкости кислорода при постоянном давлении:
для 0°С μср = 29,2741 кДж/(кмоль . К);
для 500 °С μср = 33,5488 кДж/( кмоль . К);
для 1000° С μсp = 35,9144 кДж/( кмоль . К).
По этим данным составить приближенное интерполяционное уравнение вида μср = а + bt + dt2
дающее зависимость истинной мольной теплоемкости кислорода при постоянном давлении от температуры.
Скачать решение задачи 107 (Рабинович) цена 50р
Задача 108 (Рабинович). Воздух охлаждается от 1000 °С до 100°С в процессе с постоянным давлением.
Какое количество теплоты теряет 1 кг воздуха? Задачу решить, принимая теплоемкость воздуха постоянной, а также учитывая зависимость теплоемкости от температуры. Определить относительную ошибку, получаемую в первом случае.
Ответ: 1) qCp=const= -909,63кДж/кг; 2) qCp=f(t)= - 990,1 кДж/кг; ξ = 8%.
Скачать решение задачи 108 (Рабинович) цена 50р
Задача 111 (Рабинович). В сосуде объемом 300 л находится кислород при давлении р1 = 0,2 МПа и температуре t1 = 20 °С. Какое количество теплоты необходимо подвести, чтобы температура кислорода повысилась до t2 = 300 °С? Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры принять нелинейной.
Ответ: p2=0.39 МПа
Скачать решение задачи 111 (Рабинович) цена 50р
Задача 112 (Рабинович). Найти количество теплоты, необходимое для нагрева 1 м3 (при нормальных условиях) газовой смеси состава rCO2 = 14,5%, rO2 = 6,5%, rN2 = 79,0% от 200 до 1200°С при р = const и нелинейной зависимости теплоемкости от температуры.
Ответ: qp =1582.2 кДж/м3
Скачать решение задачи 112 (Рабинович) цена 50р
Задача 113 (Рабинович). Газовая смесь имеет следующий состав по объёму: СO2=0.12; O2=0.07; N2=0.75; H2O=0.06. Определить среднюю массовую теплоемкость срт, если смесь нагревается от 100 до 300° С.
Отв. срт= 1,0684 кДж/(кг. К).
Скачать решение задачи 113 (Рабинович) цена 50р
Задача 114 (Рабинович). В регенеративном подогревателе газовой турбины воздух нагревается от 150 до 600°С. Определить количество тепла, сообщенное воздуху в единицу времени, если расход его составляет 360 кг/ч. Зависимость теплоемкости от температуры принять нелинейной.
Ответ: Qp =47,84 кДж/сек =41142,4 ккал/ч.
Скачать решение задачи 114 (Рабинович) цена 50р
Задача 115 (Рабинович). В калориметре с идеальной тепловой изоляцией находится вода в количестве Мв = 0,8 кг при температуре t = 15 °С. Калориметр изготовлен из серебра, теплоемкость которого сс = 0,2345 кДж/(кг . К).
Масса калориметра Мс — 0,25 кг. В калориметр опускают 0,2 кг алюминия при температуре ta = 100 °С. В результате этого температура воды повышается до tn = 19,24° С. Определить теплоемкость алюминия.
Ответ: са=0,8946 кДж/(кг . К)
Скачать решение задачи 115 (Рабинович) цена 50р
Задача 116 (Рабинович). Продукты сгорания топлива поступают в газоход парового котла при температуре газов t'Г = 1100 °С и покидают газоход при температуре t’’Г=700°С. Состав газов по объему: rСO2 = 11%; rO2 = 6%; rH2O =8%; rN2 = 75%. Определить, какое количество теплоты теряет 1 м3 газовой смеси, взятой при нормальных условиях.
Отв. Qp= 658,8 кДж/м3.
Скачать решение задачи 116 (Рабинович) цена 50р
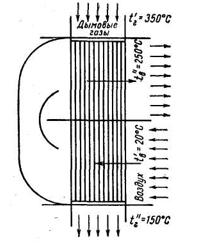
Задача 117 (Рабинович). Для использования теплоты газов, уходящих из паровых котлов, в газоходах последних устанавливают воздухоподогреватели. Газы протекают внутри труб и подогревают воздух, проходящий поперек тока (рис. 7).
При испытании котельного агрегата были получены следующие данные: температура газов соответственно на входе и на выходе из воздухоподогревателя t'Г= 350 °С, t’’Г =160 °С;
температура воздуха соответственно на входе и на выходе из воздухоподогревателя t'B =20° С, t’'B= 250°С; объемный состав газов, проходящих через воздухоподогреватель; СО2 = 12%; О2 = 6%; Н2О = 8%; N2. = 74%; расход газов VГН = 66 000 м3/ч.
Определить расход воздуха. Принять, что вся отданная газами теплота воспринята воздухом. Потерями давления воздуха в воздухоподогревателе пренебречь.
Ответ. VBН = 59500 м3/ч.
Скачать решение задачи 117 (Рабинович) цена 50р
Задача 118 (Рабинович). Найти часовой расход топлива, который необходим для работы паровой турбины мощностью 25 МВт, если теплота сгорания топлива QHP= 33,85 МДж/кг и известно, что на превращение тепловой энергии в механическую используется только 35% теплоты сожженного топлива.
Ответ. 7,59 т/ч.
Скачать решение задачи 118 (Рабинович) цена 50р
Задача 119 (Рабинович). В котельной электрической станции за 20 ч работы сожжены 62 т каменного угля, имеющего теплоту сгорания 28 900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 18% теплоты, полученной при сгорании угля.
Ответ: N=4479 кВт.
Скачать решение задачи 119 (Рабинович) цена 50р
Задача 120 (Рабинович). Мощность турбогенератора 12000 кВт, к. п. д. генератора 0,97. Какое количество воздуха нужно пропустить через генератор для его охлаждения, если конечная температура воздуха не должна превышать 55 °С? Температура в машинном отделении равна 20 °С; среднюю теплоемкость воздуха срт принять равной 1,0 кДж/(кг К).
Ответ. 10,3 кг/с.
Скачать решение задачи 120 (Рабинович) цена 80р
Задача 122 (Рабинович). Теплота сгорания топлива, выражаемая в кДж/кг, может быть также выражена в кВт ч/кг. Принимая теплоту сгорания нефти равной 41 900 кДж/кг, каменного угля 29300 кДж/кг, подмосковного бурого угля 10600 кДж/кг, выразить теплоту сгорания перечисленных топлив в кВт ч/кг.
Отв. Qнефти = 11,6 кВт*ч/кг; Qугля = 8,14 кВт*ч/кг; Qб.угля = 2,94 кВт*ч/кг
Скачать решение задачи 122 (Рабинович) цена 80р
Задача 125 (Рабинович). Первая в мире атомная электростанция, построенная в СССР, превращает атомную энергию, выделяющуюся при реакциях цепного деления ядер урана, в тепловую, а затем в электрическую энергию. Тепловая мощность реактора атомной электростанции равна 30000 кВт, а электрическая мощность электростанции составляет при этом 5000 кВт. Найти суточный расход урана, если выработка электроэнергии за сутки составила 120000 кВт-ч. Теплоту сгорания урана принять равной 22,9.10е КВт-ч/кг. Определить также, какое количество угля, имеющего теплоту сгорания 25800 кДж/кг, потребовалось бы для выработки того же количества электроэнергии на тепловой электростанции, если бы к. п. д. ее равнялся к. п. д. атомной электростанции.
Отв. Вурана = 31 г/сут; Вугля = 100 т/сут.
Скачать решение задачи 125 (Рабинович) цена 80р
Задача 126 (Рабинович). Теплоемкость газа при постоянном давлении опытным путем может быть определена в проточном калориметре. Для этого через трубопровод пропускают исследуемый газ и нагревают его электронагревателем (рис. 8). При этом измеряют количество газа, пропускаемое через трубопровод, температуры газа перед и за электронагревателем и расход электроэнергии. Давление воздуха в трубопроводе принимают неизменным. Определить теплоемкость воздуха при постоянном давлении методом проточного калориметрирования, если расход воздуха через трубопровод М =690 кг/ч, мощность электронагревателя Ni = 0,5 кВт, температура воздуха перед электронагревателем Т1 = 18 °С, а температура воздуха за электронагревателем t = 20,6 °С.
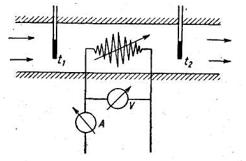
Ответ. срт= 1,0 кДж/(кг-К).
Скачать решение задачи 126 (Рабинович) цена 80р
Задача 127 (Рабинович). Метод проточного калориметрирования, описанный в предыдущей задаче, может быть также использован для определения количества газа или воздуха, протекающего через трубопровод. Найти часовой расход воздуха М кг/ч, если мощность электронагревателя Nл= 0,8 кВт, а приращение температуры воздуха t2—t1=1,8°С. Определить также скорость воздуха с в трубопроводе за электронагревателем, если давление воздуха 120 кПа, температура его за электронагревателем 20,2 °С, а диаметр трубопровода 0,125 м.
Ответ. М = 1600 кг/ч; с = 25,4 м/с.
Скачать решение задачи 127 (Рабинович) цена 80р
Задача 128 (Рабинович). При испытании двигателей внутреннего сгорания широким распространением пользуются так называемые гидротормоза. Работа двигателя при торможении превращается в теплоту трения, и для уменьшения нагрева тормозного устройства применяют водяное охлаждение. Определить часовой расход воды на охлаждение тормоза, если мощность двигателя N = 33 кВт, начальная температура воды t1B = 15 °С, конечная t2В = 60 °С; принять, что вся теплота трения передается охлаждающей воде.
Ответ. Мвот= 632 кг/ч.
Скачать решение задачи 128 (Рабинович) цена 80р
Задача 129 (Рабинович). При испытании нефтяного двигателя было найдено, что удельный расход топлива равен 231 г/(кВт ч). Определить эффективный к. п. д. этого двигателя, если теплота сгорания топлива QНР= 41 000 кДж/кг (9800 ккал/кг).
Ответ. ηе = 0,38.
Скачать решение задачи 129 (Рабинович) цена 80р
Задача 130 (Рабинович). Паросиловая установка мощностью 4200 кВт имеет к. п. д. ηст = 0,20. Определить часовой расход топлива, если его теплота сгорания Qh = 25 000 кДж/кг.
Ответ: bчас=3024 кг/ч
Скачать решение задачи 130 (Рабинович) цена 50р
Задача 131 (Рабинович). В котельной электростанции за 10 ч работы сожжено 100 т каменного угля с теплотой сгорания QНР= 29300 кДж/кг. Найти количество выработанной электроэнергии и среднюю мощность станции, если к. п. д. процесса преобразования тепловой энергии в электрическую составляет 20%.
Ответ. 162780 кВт-ч; Nср= 16278 кВт.
Скачать решение задачи 131 (Рабинович) цена 80р
Задача 132 (Рабинович). В сосуд, содержащий 5 л воды при температуре 20 °С, помещен электронагреватель мощностью 800 Вт. Определить, сколько времени потребуется, чтобы вода нагревалась до температуры кипения 100 °С. Потерями теплоты сосуда в окружающую среду пренебречь.
Ответ. t = 35 мин.
Скачать решение задачи 132 (Рабинович) цена 80р
Задача 138 (Рабинович). Найти изменение внутренней энергии 1кг воздуха при переходе его от начального состояния t1 = 300 °С до конечного при t2 = 50 °С. Зависимость теплоемкости от температуры принять линейной. Ответ дать в кДж.
Ответ: ∆u=-185,3 кДж/кг
Скачать решение задачи 138 (Рабинович) цена 50р
Задача 142 (Рабинович). В двух разобщенных между собой сосудах А и В (рис. 9) содержатся следующие газы: в сосуде А — 50 л азота при давлении р х = 2 МПа и температуре t1 = 200° С, в сосуде В — 200 л углекислого газа при давлении р2 = 0,5 МПа и температуре t2 = 600° С. Определить давление и температуру, которые установятся после соединения сосудов. Теплообменом с окружающей средой пренебречь.
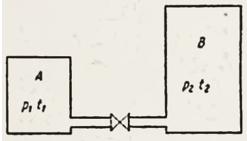
Скачать решение задачи 142 (Рабинович) цена 50р
Задача 152 (Рабинович). В закрытом сосуде заключен газ при разрежении р1 = 6667 Па и температуре t1 = 70°С. Показание барометра - 101 325 Па. До какой температуры нужно охладить газ, чтобы разрежение стало р2 = 13 332 Па?
Ответ. t2 = 45,80C.
Скачать решение задачи 152 (Рабинович) цена 50р
Задача 156 (Рабинович). В закрытом сосуде емкостью V = 0,6 м3 содержится воздух при давлении p1 =0,5 МПа и температуре t1 = 20°С. В результате охлаждения сосуда воздух, содержащийся в нем, теряет 105 кДж. Принимая теплоемкость воздуха постоянной, определить, какое давление и какая температура устанавливаются после этого в сосуде.
Ответ: p2 = 0,43 МПа
Скачать решение задачи 156 (Рабинович) цена 50р
Задача 158 (Рабинович). Сосуд емкостью 90 л содержит воздух при давлении 0,8 МПа и температуре 30° С. Определить количество теплоты, которое необходимо сообщить воздуху, чтобы повысить его давление при v =соnst до 1,6 МПа. Принять зависимость с = f (t) нелинейной.
Ответ: Qv = 184,8 МПа
Скачать решение задачи 158 (Рабинович) цена 50р
Задача 162 (Рабинович). В резервуаре, имеющем объем V = 0,5 м3, находится углекислый газ при давлении р1 = 0,6 МПа и температуре t1 = 527° С. Как изменится температура газа, если отнять от него при постоянном объеме 436 кДж? Зависимость теплоемкости от температуры считать линейной.
Ответ: t2 = 2760C
Скачать решение задачи 162 (Рабинович) цена 50р
Задача 163 (Рабинович). В калориметрической бомбе емкостью 300 см3 находится кислород при давлении р1 = 2,6 МПа и температуре t1 = 22 ºС. Найти температуру кислорода t2 после подвода к нему теплоты в количестве 4,19 кДж, считая зависимость теплоемкости от температуры линейной.
Скачать решение задачи 163 (Рабинович) цена 80р
Задача 164 (Рабинович). Какое количество теплоты необходимо затратить, чтобы нагреть 2 м3 воздуха при постоянном избыточном давлении р = 0,2 МПа от t1 = 100°С до t2 = 500° С? Какую работу при этом совершит воздух? Давление атмосферы принять равным 101 325 Па.
Ответ: L = 646.3 кДж
Скачать решение задачи 164 (Рабинович) цена 50р
Задача 167 (Рабинович). В цилиндре находится воздух при давлении р = 0,5 МПа и температуре t = 400° С. От воздуха отнимается теплота при постоянном давлении таким образом, что в конце процесса устанавливается температура t2 = 0° С. Объем цилиндра, в котором находится воздух, равен 400 л. Определить количество отнятой теплоты, конечный объем, изменение внутренней энергии и совершенную работу сжатия. Зависимость теплоемкости от температуры считать нелинейной.
Ответ: L = -118,9 кДж
Скачать решение задачи 167 (Рабинович) цена 50р
Задача 169 (Рабинович). Для использования отходящих газов двигателя мощностью N = 2500 кВт установлен подогреватель, через который проходит 60 000 м3/ч воздуха при температуре t1 = 15 ºС и давлении р = 0,101 МПа. Температура воздуха после подогревателя равна 75°С.
Определить, какая часть теплоты топлива использована в подогревателе? К. п. д. двигателя принять равным 0,33. Зависимость теплоемкости от температуры считать линейной.
Ответ 16,2%
Скачать решение задачи 169 (Рабинович) цена 50р
Задача 173 (Рабинович). Определить, какая часть теплоты, подводимой к газу в изобарном процессе, расходуется на работу и какая — на изменение внутренней энергии.
Ответ: 28,5%
Скачать решение задачи 173 (Рабинович) цена 50р
Задача 174 (Рабинович). В цилиндре двигателя внутреннего сгорания находится воздух при температуре 500°С. Вследствие подвода теплоты конечный объем воздуха увеличился в 2,2 раза.
В процессе расширения воздуха давление в цилиндре практически оставалось постоянным. Найти конечную температуру воздуха и удельные количества теплоты и работы, считая зависимость теплоемкости от температуры нелинейной.
Ответ q = 1088,7кДж/кг, L = 266,3 кДж/кг, t2 = 1428 °С
Скачать решение задачи 174 (Рабинович) цена 50р
Задача 176 (Рабинович). К газообразным продуктам сгорания, находящимся в цилиндре двигателя внутреннего сгорания, подводится при постоянном давлении столько теплоты, что температура смеси поднимается с 500 до 1900° С. Состав газовой смеси следующий; mCO2 = 15%; mO2 = 5%; mH2O = 6%; mN2 = 74%.
Найти количество теплоты, подведенной к 1 кг газообразных продуктов сгорания, считая теплоемкость нелинейно зависящей от температуры.
Ответ: qp = 1836 кДж/кг
Скачать решение задачи 176 (Рабинович) цена 50р
Задача 179 (Рабинович). 1 кг воздуха при температуре t1 = 30° С и начальном давлении р1 = 0,1 МПа сжимается изотермически до конечного давления р2 = 1 МПа. Определить конечный объем, затрачиваемую работу и количество теплоты, отводимой от газа.
Ответ: q = — 200 кДж/кг
Скачать решение задачи 179 (Рабинович) цена 50р
Задача 190 (Рабинович). Газ расширяется в цилиндре изотермически до объема в 5 раз больше первоначального. Сравнить величины работ: полного расширения и расширения на первой половине хода поршня.
Ответ. L2/L1 = 0,684
Скачать решение задачи 190 (Рабинович) цена 50р
Задача 195 (Рабинович). 1 кг воздуха при начальной температуре t1 = 30°С и давлении p1 = 0,4 МПа сжимается адиабатно до конечного давления р2 = 1 МПа. Определить конечный объем, конечную температуру t2 и затрачиваемую работу.
Отв.: v2=0.168 м3/кг
Скачать решение задачи 195 (Рабинович) цена 50р
Задача 201 (Рабинович). В газовом двигателе смесь газа и воздуха адиабатно сжимается так, что к концу сжатия ее температура оказывается на 200° С ниже температуры самовоспламенения газа. В начале сжатия p1 = 0,09 МПа и t2 = 70° С. Показатель адиабаты k = 1,36, R = 314 Дж/(кг*К), температура самовоспламенения равна 650°С. Определить величину работы сжатия и степень сжатия ε = v1/v2.
Отв.: l= - 331,4 кДж/кг
Скачать решение задачи 201 (Рабинович) цена 50р
Задача 203 (Рабинович). Адиабатным сжатием повысили температуру воздуха в двигателе так, что она стала равной температуре воспламенения нефти; объем при этом уменьшился в 14 раз. Определить конечную температуру и конечное давление воздуха, если р1 = 0,1 МПа и t1= 1000С.
Отв.: p2= 4 МПа
Скачать решение задачи 203 (Рабинович) цена 50р
Задача 205 (Рабинович). В баллоне емкостью 100 л находится воздух при давлении p1 = 5 МПа и температуре t1 = 20°С. Давление окружающей среды р2 = 0,1 МПа. Определить работу, которая может быть произведена содержащимся в баллоне воздухом при расширении его до давления окружающей среды по изотерме и по адиабате. Найти также минимальную температуру, которую будет иметь воздух в баллоне, если открыть вентиль и выпускать воздух из баллона до тех пор, пока давление в нем не станет равным давлению окружающей среды и при условии, что теплообмен воздуха с окружающей средой будет отсутствовать.
Отв.: L= 686,4 кДж; t2 = -177
Скачать решение задачи 205 (Рабинович) цена 50р
Задача 208 (Рабинович). Воздух адиабатно расширяется в цилиндре так, что конечный его объем в 5 раз больше начального.
Сравнить работу полного расширения и расширения на первой половине хода поршня.
Скачать решение задачи 208 (Рабинович) цена 50р
Задача 209 (Рабинович). Объем воздуха при адиабатном сжатии в цилиндре двигателя внутреннего сгорания уменьшается в 13 раз. Начальная температура воздуха перед сжатием t1 = 77 °С, а начальное давление p1 = 0,9 бар. Определить температуру и давление воздуха после сжатия.
Ответ: t2 = 703 °С, p2 = 0,327 МПа.
Скачать решение задачи 209 (Рабинович) цена 50р
Задача 231 (Рабинович). 2 м3 воздуха при давлении р1 = 0,2 МПа и температуре t1 = 40° С сжимаются до давления р2 = 1,1 МПа и объема V2 = 0,5 м3. Определить показатель политропы, работу сжатия и количество отведенной теплоты.
Ответ m = 1,23; L = -652 кДж; Q = -272 кДж.
Скачать решение задачи 231 (Рабинович) цена 50р
Задача 237 (Рабинович). Определить энтропию 1 кг кислорода при р = 0,8 МПа и t = 2500 С. Теплоемкость считать постоянной.
Отв.: s = 0,0605 кДж/(кг*К)
Скачать решение задачи 237 (Рабинович) цена 50р
Задача 239 (Рабинович). Найти энтропию 1 кг кислорода при р = 0,8 МПа и t = 250° С. Теплоемкость считать, переменной, приняв зависимость ее от температуры линейной
Ответ: s = 0,0739 кДж/кг*К
Скачать решение задачи 239 (Рабинович) цена 50р
Задача 240 (Рабинович). 1 кг кислорода при температуре t1 = 127°С расширяется до пятикратного объема; температура его при этом падает до t2 = 27° С. Определить изменение энтропии. Теплоемкость считать постоянной.
Ответ: s2-s1 = 0,2324 кДж/кг*К
Скачать решение задачи 240 (Рабинович) цена 50р
Задача 242 (Рабинович). 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при v = const давление повышается в 1,5 раза. Найти общее изменение энтропии воздуха. Теплоемкость считать постоянной.
Ответ: ∆s = 0,293 кДж/кг*К
Скачать решение задачи 242 (Рабинович) цена 50р
Задача 243 (Рабинович). В диаграмме Т-s для идеального газа нанесены три изобары (рис. 22). Две крайние изобары относятся к давлениям соответственно 0,1 и 10 МПа. Определить, какое давление соответствует средней изобаре.
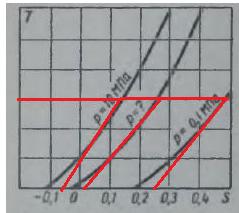
Отв. р = 2,15 МПа.
Скачать решение задачи 243 (Рабинович) цена 50р
Задача 244 (Рабинович). 10 м3 воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400° С. Сжатие производится: 1) изохорно, 2) изобарно, 3) адиабатно. Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, найти энтропию воздуха в конце каждого процесса.
Скачать решение задачи 244 (Рабинович) цена 50р
Задача 246 (Рабинович). 1 кг воздуха сжимается по политропе от 0,1 МПа и 20° С до 0,8 МПа при m = 1,2. Определить конечную температуру, изменение энтропии, количество отведенной теплоты и затраченную работу.
Ответ t2 = 141°С; = -0,2445 кДж/(кг•К); q = -87,9 кДж/кг; L = -174,2 кДж/кг.
Скачать решение задачи 246 (Рабинович) цена 50р
Задача 247 (Рабинович). 1 кг воздуха, находящемуся в состоянии А (рис. 23), сообщается теплота один раз при р = const и другой — при v = const так, что в обоих случаях конечные температуры одинаковы. Сравнить изменение энтропии в обоих процессах, если t1 = 15° С и t2 = 500° С. Теплоемкость считать переменной, приняв зависимость ее от температуры линейной.
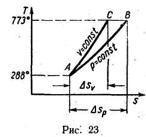
Ответ: 1,38
Скачать решение задачи 247 (Рабинович) цена 50р
Задача 249 (Рабинович). Построить в диаграмме Ts для 1 кг воздуха в пределах от 0 до 200° С изохоры: v1 = 0,2 м3/кг; v2 = 0,4 м3/кг, v3 = 0,6 м3/кг. Теплоемкость считать постоянной.
Скачать решение задачи 249 (Рабинович) цена 50р
Задача 251 (Рабинович). 1 кг воздуха при р1 = 0,9 МПа и t1 = 100 С сжимается по адиабате до р2 = 3,7 МПа. Пользуясь диаграммой Ts, найти конечную температуру, а также то давление, до которого нужно сжать воздух, чтобы температура его стала. t3 = 80° С.
Ответ: 2,08 МПа.
Скачать решение задачи 251 (Рабинович) цена 50р
Задача 253 (Рабинович). 1 кг воздуха при Р1 = 0,09 МПа и t1 = 100° С сжимается по адиабате так, что его объем уменьшается в 16 раз.
Найти конечную температуру и конечное давление, пользуясь диаграммой Тs.
Ответ t2 = 858°С; = 0 кДж/(кг•К); Р2 = 4,365 МПа.
Скачать решение задачи 253 (Рабинович) цена 50р
Задача 254 (Рабинович). В сосуде объемом 300 л заключен воздух при давлении р1 =5 МПа и температуре t1 = 20° С. Параметры среды: р0 = 0,1 МПа, t0= 20° С.
Определить максимальную полезную, работу, которую может произвести сжатый воздух, находящийся в сосуде. Представить процесс в диаграмме pv.
Ответ: Lmax = 4377 кДж
Скачать решение задачи 254 (Рабинович) цена 50р
Задача 255 (Рабинович). В сосуде объемом 200 л находится углекислота при температуре t1 = 20° С и давлении Р1 = 10 МПа. Температура среды t0 = 20° С, давление среды Р0 = 0,1 МПа. Определить максимальную полезную работу, которую может произвести находящаяся в сосуде углекислота
Ответ Lmax.полез=7226,2кДж
Скачать решение задачи 255 (Рабинович) цена 50р
Задача 257 (Рабинович). Определить максимальную полезную работу, которая может быть произведена 1 кг кислорода, если его начальное состояние характеризуется параметрами t1 = 400° С и р1 = 0,1 МПа, а состояние среды — параметрами t0 = 20° С и р0 = 0,1 МПа. Представить процесс в диаграммах pv и Ts.
Отв. Lmax (полезн) = 4600 Дж.
Скачать решение задачи 257 (Рабинович) цена 50р
Задача 258 (Рабинович). В сосуде объемом 400 л заключен воздух при давлении Р1 = 0,1 МПа и температуре t1 = -40° С. Параметры среды; Р0 = 0,1 МПа и t0 = 20° С.
Определить максимальную полезную работу, которую может произвести воздух, заключенный в сосуде. Представить процесс в диаграммах рv и TS
Отв. Lmax (полезн) = 30658 Дж.
Скачать решение задачи 258 (Рабинович) цена 50р
Задача 259 (Рабинович) К газу в круговом процессе подведено 250 кДж теплоты. Термический к. п. д. равен 0,46. Найти работу, полученную за цикл.
Отв. L=115 кДж.
Скачать решение задачи 259 (Рабинович) цена 50р
Задача 260 (Рабинович). В результате осуществления кругового процесса получена работа, равная 80 кДж, а отдано охладителю 50 кДж теплоты. Определить термический к. п. д. цикла.
Отв. ηt = 0,615.
Скачать решение задачи 259 (Рабинович) цена 50р
Задача 261 (Рабинович). 1 кг воздуха совершает цикл Карно (см. рис. 31) в пределах температур t1 = 627°С и t2 = 27°С, причем наивысшее давление составляет 6 МПа, а наинизшее — 0,1 МПа. Определить параметры состояния воздуха в характерных точках цикла, работу, термический к. п. д. цикла и количество подведенной и отведенной теплоты.
Скачать решение задачи 261 (Рабинович) цена 50р
Задача 262 (Рабинович). 1 кг воздуха совершает цикл Карно в пределах температур t1= 250° С и t2 = 30° С. Наивысшее давление Р1 = 1 МПа, наинизшее р3 = 0,12 МПа. Определить параметры состояния воздуха в характерных точках, количества подведенной и отведенной теплоты, работу и термический к. п. д. цикла.
Отв. v1 = 0,15 м3/кг; v2= 0,185 м3/кг; v3 = 0,725 м3/кг; v4 = 0,59 м3/кг; р2= 0,81 МПа; р4 = 0,15 МПа; ηt= 0,42; l0= 18,1 кДж/кг; q1 = 31,l кДж/кг; q2= 18 кДж/кг.
Скачать решение задачи 262 (Рабинович) цена 50р
Задача 264 (Рабинович). Для идеального цикла поршневого двигателя внутреннего сгорания с подводом теплоты при v = const определить параметры в характерных точках, полученную работу, термический к. п. д., количество подведенной и отведенной теплоты, если дано: p1 = 0,1 МПа; t1 = 20°С; ε = 3,6; λ = 3,33; k = 1,4. Рабочее тело — воздух. Теплоемкость принять постоянной.
Скачать решение задачи 264 (Рабинович) цена 50р
Задача 268 (Рабинович). 1 кг воздуха работает по циклу, изображенному на рис. 53. Начальное давление воздуха р1 = 0,1 МПа, начальная температура t1 = 27°С, а степень сжатия ε = 5. Количество теплоты, подводимой во время изохорного сжатия, равно 1300 кДж/кг. Определить параметры воздуха в характерных точках и полезную работу цикла. Теплоемкость воздуха считать постоянной.
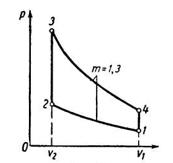
Скачать решение задачи 268 (Рабинович) цена 50р
Задача 270 (Рабинович). Температура воспламенения топлива, подаваемого в цилиндр двигателя с изобарным подводом теплоты, равна 800°С. Определить минимально необходимое значение степени сжатия ε, если начальная температура воздуха t1 = 77° С. Сжатие считать адиабатным, k= 1,4.
Отв. ε = 16,4.
Скачать решение задачи 270 (Рабинович) цена 50р
Задача 271 (Рабинович). Для цикла с подводом теплоты при р = const (рис. 54) найти параметры в характерных точках, полезную работу, термический к. п. д., количество подведенной и отведенной теплоты, если дано: р1 = 0,1 МПа; t1 = 20°С; ε = 12,7; k = 1,4. Рабочее тело — воздух. Теплоемкость считать постоянной.
Скачать решение задачи 271 (Рабинович) цена 50р
Задача 273 (Рабинович). Найти давление и объем в характерных точках цикла поршневого двигателя внутреннего сгорания с подводом теплоты при р = const, а также термический к. п. д. и полезную работу, если дано: р1 = 100 кПа, ε = 14; р = 1,5; к = 1,4. Диаметр цилиндра d = 0,3 м, ход поршня S = 0,45 м. Рабочее тело - воздух. Теплоемкость считать постоянной.
Отв. V1= V4= 0,03416 м3; V2 = 0,00244 м3; V3 = 0,00366 м3; р2= 4,02 МПа; р4 = 0,176 МПа, ηt = 0,65.
Скачать решение задачи 273 (Рабинович) цена 50р
Задача 282 (Рабинович). Для идеального цикла газовой турбины с подводом теплоты при р = const (см. рис. 39) найти параметры в характерных точках, полезную работу, термический к. п. д., количество подведенной и отведенной теплоты, если дано: р1 = 100 кПа; t1 = 27°С; t3 = 700°С; λ = p2/p1 = 10, k = 1,4. Рабочее тело— воздух. Теплоемкость принять постоянной.
Скачать решение задачи 282 (Рабинович) цена 50р
Задача 283 (Рабинович). Для идеального цикла газовой турбины с подводом теплоты при р =const (см. рис. 39) определить параметры в характерных точках, полезную работу, термический к. п. д., количество подведенной и отведенной теплоты. Дано: р1 = 0,1 МПа; t1= 17°С; t3= 600°С; λ = p2/p1 = 8. Рабочее тело - воздух. Теплоемкость принять постоянной.
Отв. v1= 0,831 м3/кг; v2 = 0,189 м3/кг; v3= 0,313 м3/кг; v4 = 1,38 м3/кг; t2= 254°С; р, = р3= 0,8 МПа; q1= 350 кДж/кг; q2 = 192,2 кДж/кг; ηt= 0,45.
Скачать решение задачи 283 (Рабинович) цена 50р
Задача 284 (Рабинович). Газовая турбина работает по циклу с подводом теплоты при р = const. Известны параметры: р1 = 0,1 МПа; t1 =40 °C; t4 = 400 °С, а также степень увеличения давления λ = 8. Рабочее тело - воздух. Определить параметры в характерных точках цикла, количество подведенной и. отведенной теплоты, работу, совершаемую за цикл, и термический к. п. д. Теплоемкость считать постоянной.
Отв. v1 = 0,9 м3/кг; р2 = 0,8 МПа; v2= 0,204 м3/кг; t2= 297° С; v3= 0,438 м3/кг; t3= 948° С; v4= 1,93м3/кг; q1 = 659 кДж/кг; q2 = 364 кДж/кг; l0 = 296 кДж/кг; ηt = 0,45.
Скачать решение задачи 284 (Рабинович) цена 50р
Задача 285 (Рабинович). На рис. 60 приведена принципиальная схема газотурбинной установки, работающей с подводом теплоты при р =const и с полной регенерацией тепла. На рисунке: ТН — топливный насос; КС—камера сгорания; ГТ — газовая турбина; ВК — воздушный компрессор; ПД — пусковой двигатель; Р — регенеративный подогреватель.
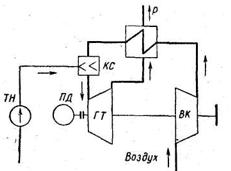
Цикл этой установки представлен на рис. 42. Известны параметры t1= 30° С и tb= 400° С, а также степень повышения давления в цикле λ = 6. Рабочее тело — воздух.
Отв. ηt = 0,55; экономия составляет 37,5%.
Скачать решение задачи 285 (Рабинович) цена 50р
Задача 286 (Рабинович). Газовая турбина работает по циклу с подводом тепла при р = const без регенерации (см. рис. 39). Известны степень повышения давления в цикле λ = p2/p1 = 7 и степень предварительного расширения ρ = v3/v2 = 2,4. Рабочее тело - воздух. Найти термический к. п. д. этого цикла и сравнить его с циклом поршневого двигателя внутреннего сгорания с подводом теплоты при р = const при одинаковых степенях сжатия ε и при одинаковых степенях расширения ρ. Представить цикл в диаграмме Ts.
Отв. ηt ГТ = 0,426; ηt ПД = 0,275.
Скачать решение задачи 286 (Рабинович) цена 50р
Задача 287 (Рабинович). Газотурбинная установка работает с подводом теплоты при v = const и с полной регенерацией. Известны параметры: t1 = 30° С и t5 = 400° С, а также λ = p2/p1 = 4. Рабочее тело - воздух. Определить термический к. п. д. этого цикла. Изобразить цикл в диаграмме Ts.
Отв. ηt = 0,585.
Скачать решение задачи 287 (Рабинович) цена 50р
Задача 288 (Рабинович). Построить график зависимости термического к. п. д., идеального цикла газовой турбины с подводом теплоты при р = const для λ = 2, 4, 6, 8 и 10.
Скачать решение задачи 288 (Рабинович) цена 50р


