Элементы линейной алгебры и аналитической геометрии.
1. Даны векторы a ={2 ;d+1; γ}, b ={c; 2-α; c-1}, c ={α; α; 2-γ}, d ={2+c+α; d+3; c+1} в декартовой системе координат. Показать, что векторы а, b, c образуют базис. Найти координаты вектора d в этом базисе (написать разложение вектора d по векторам a, b, c).
2. Даны координаты вершин пирамиды А1(с; -d; 1), А2(γ+1; c; d+1), А3 (-1; d; 0), А4(d; 1;-Υ).
Найти: 1) длину ребра А1А2;2) угол между ребрами А1А2 и А1А3; 3) угол между ребром А1А2 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
3. Пусть даны векторы a ={c, d-α, α+5}, b ={2-γ, -d, c+d}. Найти
а) скалярное и векторное произведение векторов k =αa -γb и m =-(3+α)a +(d-γ)b ,
б) угол между векторами k и m .
в) длину и направляющие косинусы вектора m .
4-13. Привести уравнения к каноническому виду, определить тип кривой и построить ее.
4. x2-y2+4x-6y-30=0 5. 3x2+5y2+18x-10y-13=0
6. x2-4x-y-5=0 7. -2x2+y2-4x+2y-5=0
8. 3x2+y2-12x+6y-13=0 9. 6x2+y2-244x=0
10. 2y2+4x-4y-6=0 11. x2 -6x+y-1=0
12. 3x2-y2+6x-4y-2=0 13. 5x2+2y2+30x-8y-7=0.
14.-23. Построить кривую в полярной системе координат.
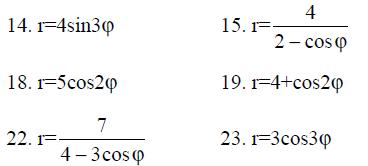
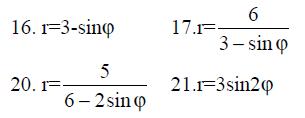
24. Решить систему линейных уравнений двумя способами: методом Гаусса и методом Крамера.
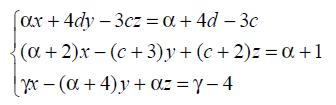
25.-34. Решить однородную систему уравнений
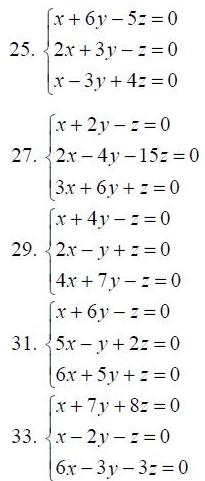
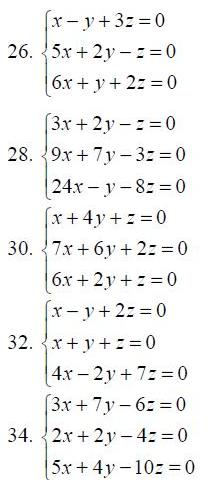
35.-43. Дано тригонометрическое число а. Требуется: записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z5=a2.
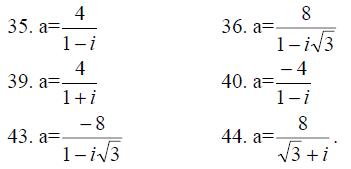
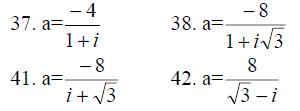
Введение в математический анализ
45.-54. Найти указанные пределы, не пользуясь правилом Лопиталя.
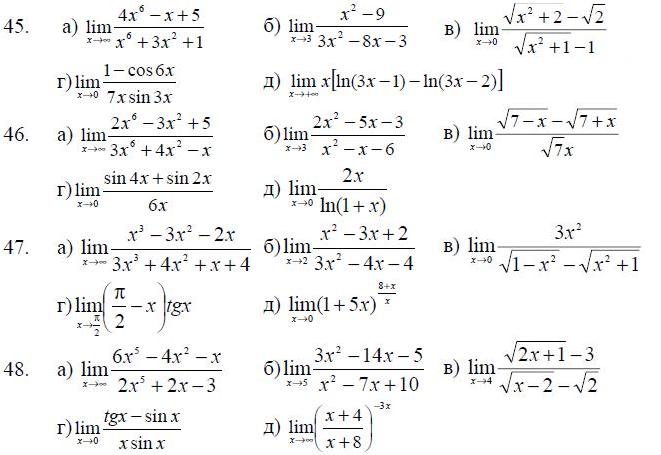
55.-64. Задана функция y=f(x) и два значения аргумента х1 и х2.Требуется: 1) установить, является ли эта функция напрерывной или разрывной для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее пределы справа и слева;
3) сделать схематический чертеж.
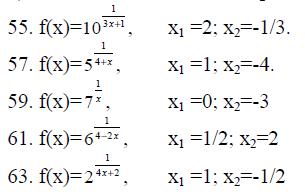
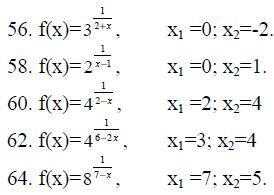
65.-74.Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
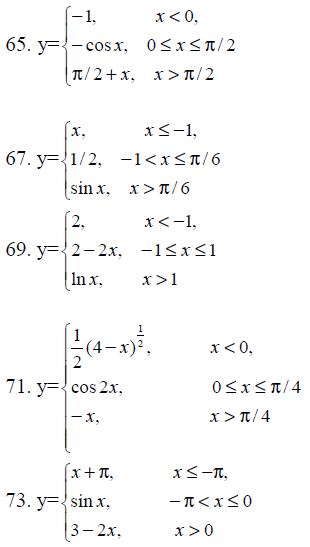
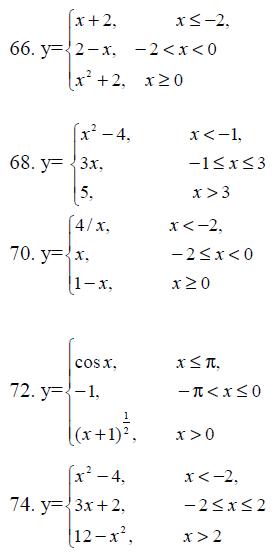
Производная и ее приложения
75.-84. Найти производные dy/dx для данных функций.
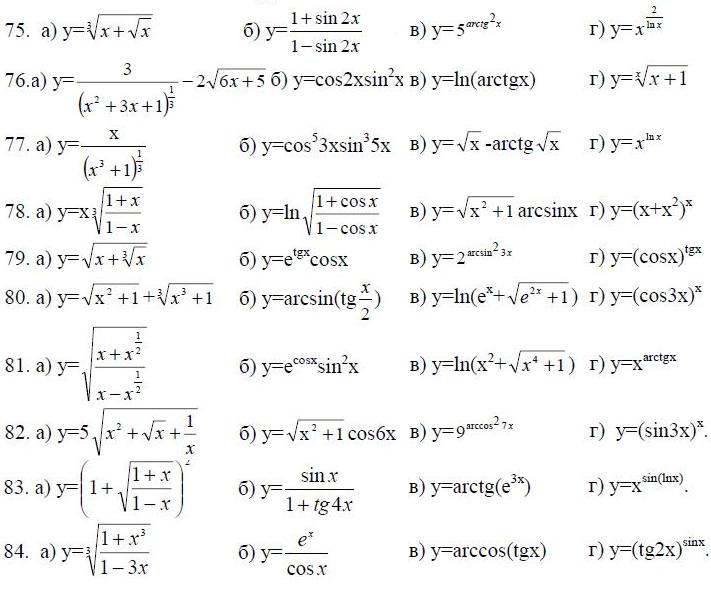
85.-94. Для данных функций найти dy/dx, d2y/dx2
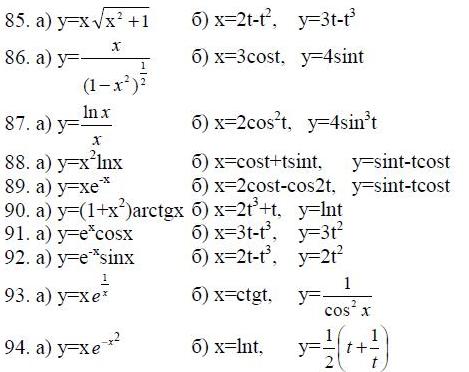
95.-104. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции f(x)=ex вычислить значение ea с точностью 0.001.
95. а=0.49 96. а=0.36 97. а=0.13 98. а=0.83 99. а=0.59
100. а=0.53 101. а=0.78 102. а=0.21 103. а=0.15 104. а=0.72
105. -114. Пользуясь правилом Лопиталя, вычислить пределы.
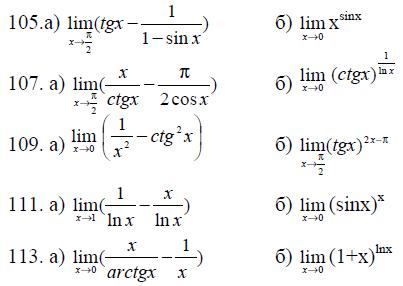
115.-124. Найти наименьшее и наибольшее значение функции y=f(x) на отрезке [a,b].
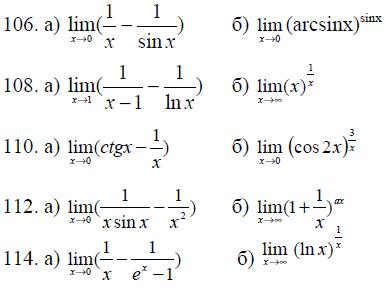
Приложения дифференциального исчисления
125.-144. Исследовать методами дифференциального исчисления функцию и построить ее график.
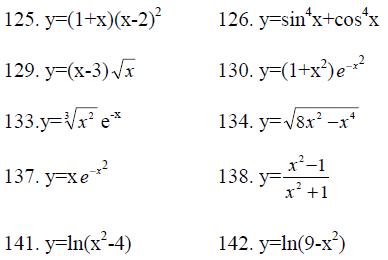
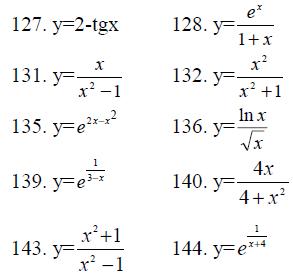
145.-154. Написать уравнения касательной и нормали к кривой y=f(x) в точке М0(x0,y0).
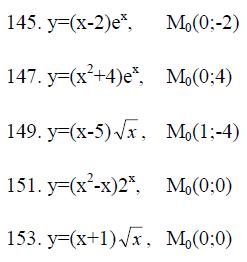
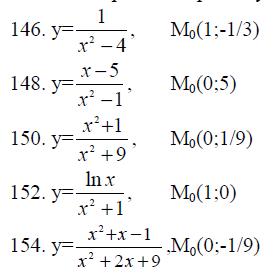
155.- 164. Вычислить приближенно с помощью дифференциала.
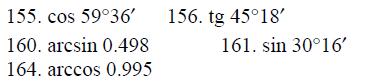
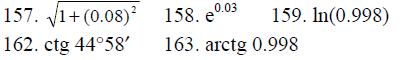
Дифференциальное исчисление функций нескольких переменных
165.-174. Построить поверхности, заданные уравнениями.
165. x2+z2=4;
166. y2-x2=1
167. 9x2+16y2=144
168. x2+y2=2x
169. y2+2y=z;
170. z2+y2-3x2=1
171. x2-3y2-2z2=1
172. 5x2+y2+2z2=1
173 x2+2y2-3z2=0
174. 3y2+z2=-x.
Дифференциальное исчисление функций нескольких переменных часть 1
175.-184. Найти области определения функций
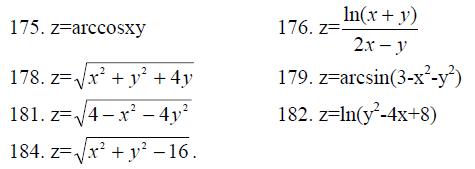
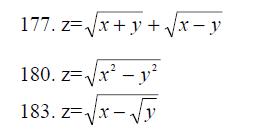
185.-194. Вычислить частные производные dz/dx и dz/dy от функций
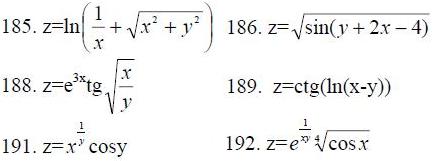
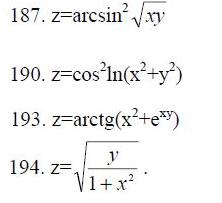
195.-204. Вычислить производные от сложных функций.
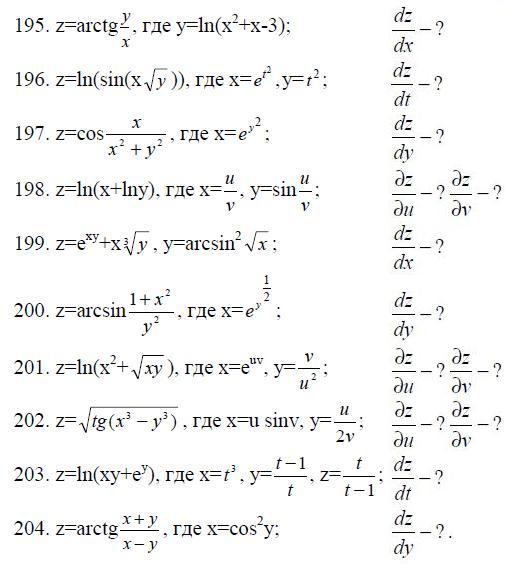
205.-214. Вычислить частные производные dz/dx и dz/dyот функций, заданных неявно.
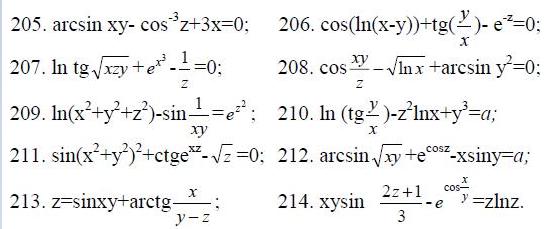
215.- 224. Даны функция z=z(x, y), точка М0(x0, y0) и вектор а.
Найти
1) grad z в точке М0,
2) производную z в точке М0 по направлению вектора а.
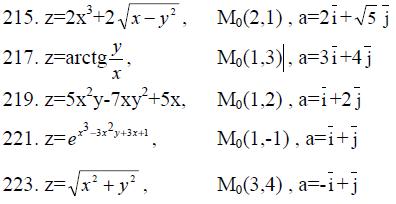
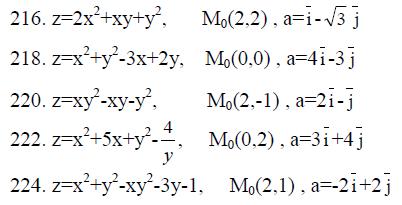
225-234. Найти неопределенные интегралы.
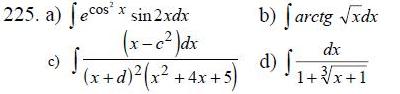
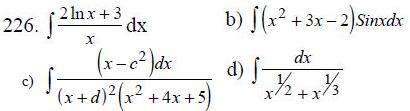
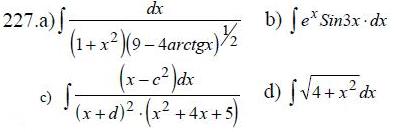
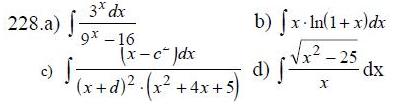
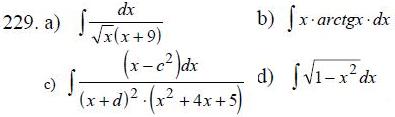
235-244. Вычислить определенные интегралы:
245-254. Вычислить несобственный интеграл или доказать его расходимость.
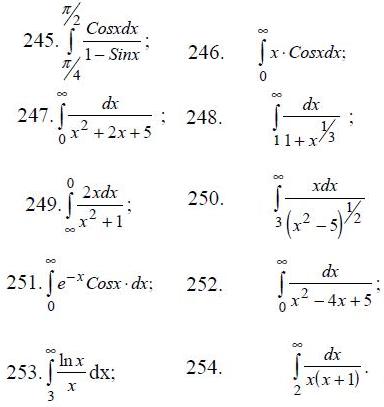
255-264. Вычислить площадь фигуры, ограниченной данными кривыми.
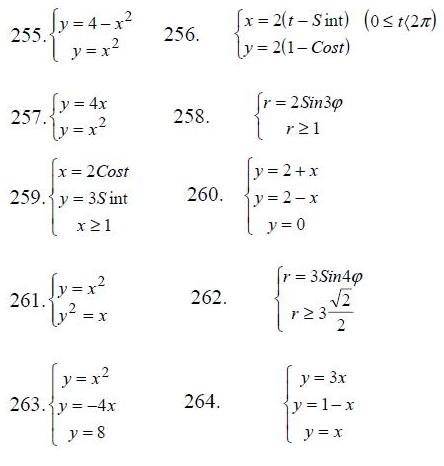
265-274.Найти общее решение линейного ДУ.
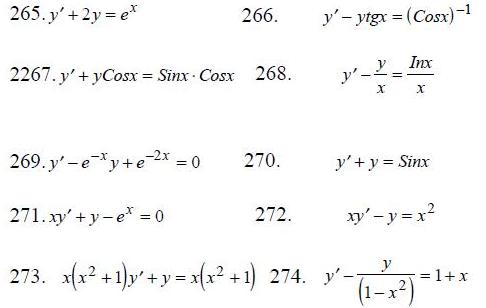
275-284. Найти общее решение ДУ.
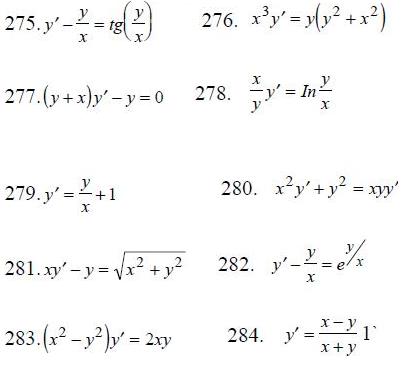
285-294. Найти общее решение уравнения 2-го порядка
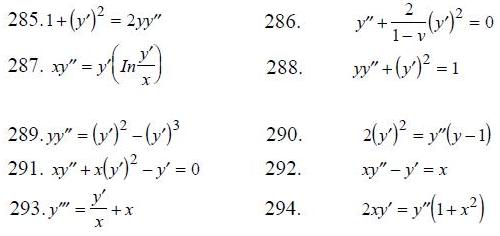
295-304. Найти частное решение ДУ, удовлетворяющее данными начальными условиями (решение задачи Коши).
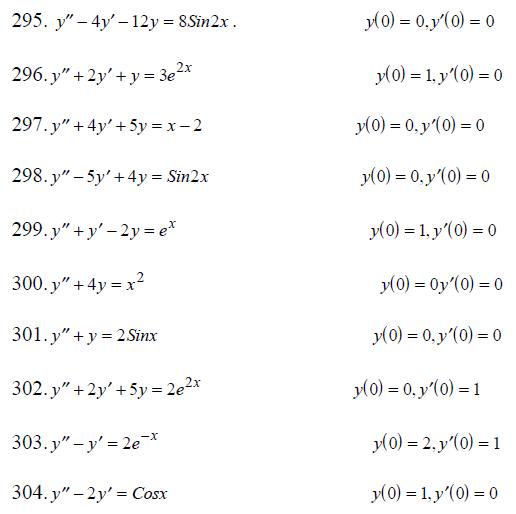
305-314. Найти общее решение системы ДУ.
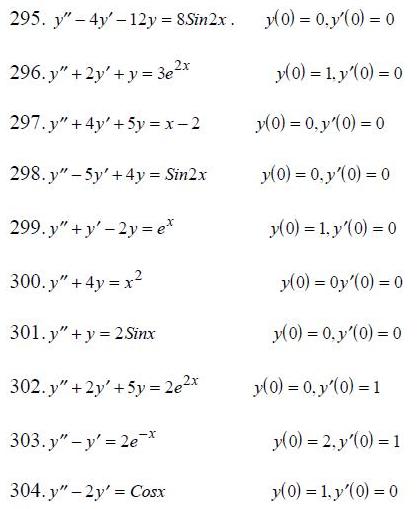
371-380. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривыми, заданными уравнениями в декартовых координатах.
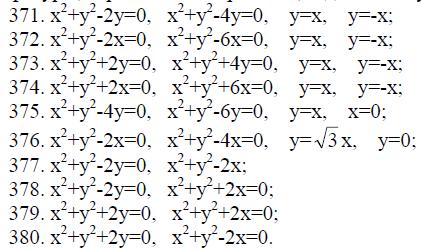
381-390. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями.
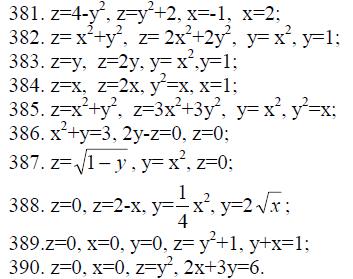
391-400. Вычислить криволинейные интегралы
391. Вычислить криволинейный интеграл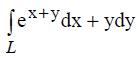 
по контуру L, где L- ломаная ОАВ: О(0;0); А(4;0); В(0;2).
392. Вычислить криволинейный интеграл 
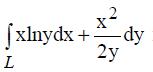по пути L, где L- некоторый путь, соединяющий точки А(1;е); В(2;е2).
393. Вычислить криволинейный интеграл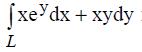 
по дуге параболы у=х2 от точки точки А(1;1); В(2;4).
394. Вычислить криволинейный интеграл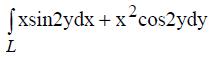 
по пути, соединяющему точку А(1;π/6) с точкой В(0;π/4).
395. Вычислить криволинейный интеграл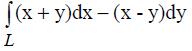 
по контуру L: x=4cost, y=4sint, π/2≤t≤π
396. Вычислить криволинейный интеграл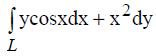 
по дуге параболы у=х2 от точки А(0;0); В(π/4; π2/16).
397. Вычислить криволинейный интеграл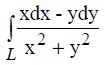 
по контуру L: x=2cost, y=2sint,
398. Вычислить криволинейный интеграл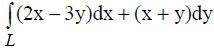 
по контуру L, где L-ломаная ОАВ: О(0;0); А(2;0); В(0;4).
399. Вычислить криволинейный интеграл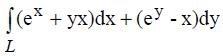 
по отрезку прямой, соединяющей точки А(2;1), В(-2;2).
400. Вычислить криволинейный интеграл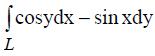 
взятый вдоль отрезка прямой, соединяющей точки А(2;-2), В(-2;2).
401-410. Вычислить криволинейные интегралы по замкнутому контуру с помощью формулы Грина.
401. По формуле Грина вычислить криволинейный интеграл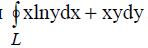 
взятый по замкнутому контуру L: у=1, у=2, х=0, ху=1.
402. По формуле Грина вычислить криволинейный интеграл L- контур прямоугольника с вершинами: А(1;1), В(2;2), С(2;-1), D(1;-2).
403. По формуле Грина вычислить криволинейный интеграл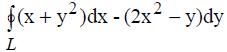 
взятый по замкнутому контуру L: у=х2, у=3.
404. По формуле Грина вычислить криволинейный интеграл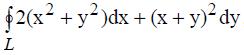 
где L- контур треугольника с вершинами: А(1;1), В(2;2), С(1;2).
405. По формуле Грина вычислить криволинейный интеграл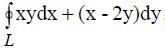 
взятый по замкнутому контуру L: у2+х2=1
406. По формуле Грина вычислить криволинейный интеграл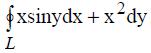 
взятый по замкнутому контуру L: у=х2, у=2, х=0 (х≥0).
407. По формуле Грина вычислить криволинейный интеграл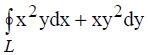 
взятый по замкнутому контуру L: у-х=0, у+х=0, х=(4-y2)0,5
408. По формуле Грина вычислить криволинейный интеграл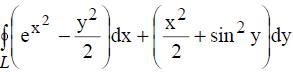 
где L - контур, ограниченный линиями: y=x, y=-1, x=L.
409. По формуле Грина вычислить криволинейный интеграл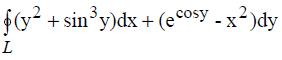 
взятый по замкнутому контуру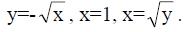 
410. По формуле Грина вычислить криволинейный интеграл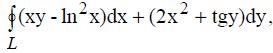 
взятый по замкнутому контуру L: у+х=1, у=0,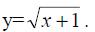 
421-430. Исследовать сходимость числового ряда.
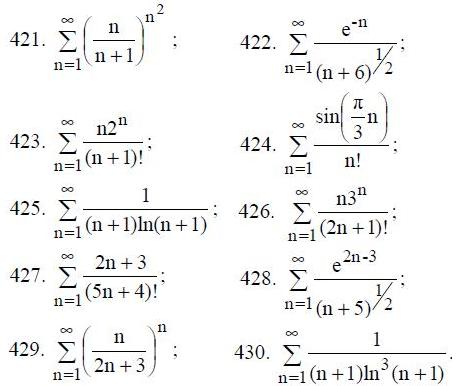
431-440. Найти интервал сходимость степенного ряда.
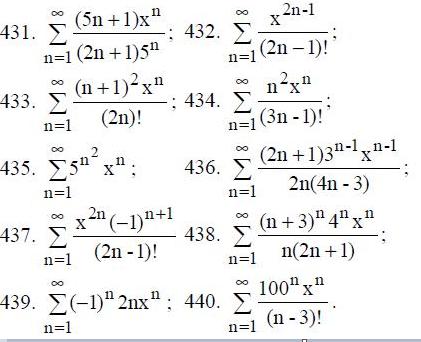
441-450. С помощью разложения в ряд подынтегральной функции вычислить определенный интеграл с погрешностью 0.001.
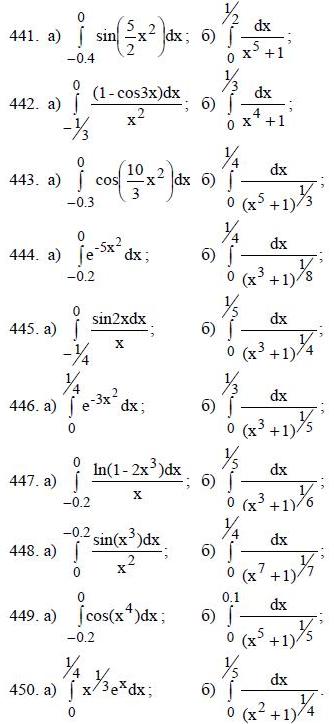
451-460. Найти три первых, отличных от 0, члена разложения в ряд Тейлора решения дифференциального уравнения f((x, y, y)=0, удовлетворяющего начальному условию у(0)=у0.
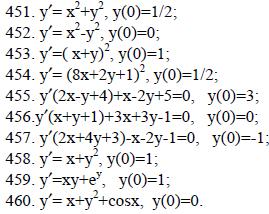
Cтраница 1 из 2