Математическое моделирование химико-технологических процессов
Задача 1.1 В таблице 1.1 приведены данные разгонки широкой бензиново фракции. Постройте серию эмпирических моделей в виде алгебраических степенных полиномов от первой до 5 степени. Оцените адекватность каждой модели, рассчитав коэффициент детерминации, остаточную сумму.
Таблица 1.1 (начало)
|
Доля отгона, % |
2,84 |
6,19 |
10,22 |
15,09 |
20,82 |
27,15 |
33,68 |
40,10 |
46,36 |
52,53 |
|
ТНК, оС |
0.2 |
11.4 |
22.6 |
33.8 |
44.9 |
56.1 |
67.3 |
78.5 |
89.7 |
100.8 |
Таблица 1.1 (продолжение)
|
Доля отгона, % |
58,69 |
64,89 |
71,09 |
77,07 |
82,53 |
87,25 |
91,25 |
94,63 |
97,51 |
|
ТНК, оС |
112 |
123.2 |
134.4 |
145.6 |
156.7 |
167.9 |
179.1 |
190.3 |
201.5 |
Скачать задачу 1.1 (моделирование процессов) цена 100р
Задача 1.2 По приведенным в Таблице 1.2 данным зависимости плотности указанных жидкостей от температуры построить эмпирическую модель и оценить её адекватность. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.2 - Плотность в кг/м3 при указанной температуре в ºС
|
Вар |
Вещество |
-20 |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
0 |
Ацетон |
835 |
813 |
791 |
768 |
746 |
719 |
693 |
665 |
Скачать задачу 1.2 (моделирование процессов) цена 100р
Задача 1.3 В Таблице 1.3 приведены зависимости вязкости жидкости от температуры для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.3 - Динамическая вязкость в мПа*с при указанной температуре в ºС
|
Вещ-во |
Динамическая вязкость в мПа*с при указанной температуре в °С |
|||||||||||
|
-20 |
-10 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
120 |
|
|
Ацетон |
0,5 |
0,442 |
0,395 |
0,356 |
0,322 |
0,293 |
0,268 |
0,246 |
0,23 |
0,2 |
0,17 |
0,15 |
Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков.
Скачать задачу 1.3 (моделирование процессов) цена 100р
Задача 1.4 В Таблице 1.4 приведены зависимости удельной теплоты парообразования (в кДж/кг) от температуры (в оС) для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.4 - Теплота парообразования кДж/кг от температуры в ºС
|
Вар |
Вещ-во |
0 |
20 |
60 |
100 |
140 |
|
0 |
Ацетон |
566 |
553 |
520 |
474 |
- |
Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков.
Скачать задачу 1.4 (моделирование процессов) цена 100р
Задача 1.5 Зависимость константы скорости реакции от температуры для ряда веществ приведена в Таблице 1.5. Рассмотрите возможность описания этой зависимости уравнением Аррениуса. По приведенным данным определите константы уравнения Аррениуса – энергию активации и предэкспоненциальный фактор. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
Таблица 1.5 - Константа скорости реакции в с-1 от температуры в ºС
|
Вар |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
|
0 |
0,05 |
0,25 |
0,6 |
0,98 |
1,35 |
1,99 |
2,87 |
4,56 |
8,43 |
Скачать задачу 1.5 (моделирование процессов) цена 100р
Задача 1.6. В таблице 1.6. приведена зависимость теплоемкости газов от температуры для ряда веществ. Постройте по приведенным данным эмпирическую модель. Оцените адекватность модели, рассчитав коэффициент детерминации, остаточную сумму. Постройте график остатков. Задача выполняется по вариантам. Вариант выбирается согласно последней цифре в номере зачётной книжки.
|
Вар |
Вещество |
Теплоемкость в кДж/кг*К от температуры в К |
|||||||
|
273 |
300 |
500 |
700 |
900 |
1100 |
1300 |
1500 |
||
|
0 |
О2 |
0,9148 |
0,9169 |
0,9391 |
0,9688 |
0,996 |
1,0182 |
1,0371 |
1,053 |
Скачать задачу 1.6 (моделирование процессов) цена 100р
2 Физические свойства чистых веществ – уравнения состояния
Задача 2.1 Найти удельный объем н-бутана при температуре 393.3 К и давлении 16.6 атм, используя уравнение состояния Рейндлиха-Квонга. Молекула н-бутана имеет симметричное строение, поэтому уравнение Рейндлиха-Квонга должно дать результат, близкий к экспериментальному (уравнения Соаве-Рейндлиха-Квонга и Пенга-Робинсона использовать необязательно). Так как давление выше 10 атм, можно ожидать существенных отклонений от закона идеального газа. Критические параметры бутана: Tc = 425.2 K, Pc = 37.5 атм.
Скачать задачу 2.1 (моделирование процессов) цена 100р
Задача 2.2 Определите молярный объем аммиака при давлении 56 атм и температуре 450 К, используя уравнение Рейндлиха-Квонга. Критические показатели для аммиака TС = 405.5 К, РС = 111.3 атм, a = 4.2527, b = 0.02590. Единицы измерения a и b соответствуют v, измеряемому в л/(г моль).
Скачать задачу 2.2 (моделирование процессов) цена 100р
Задача 2.3 Решите задачу №2.2, используя уравнения Соаве-Рейндлиха-Квонга и Пенга- Робинсона. Ацентрический фактор для молекулы аммиака принять равным 0.25. Объясните различия.
Скачать задачу 2.3 (моделирование процессов) цена 100р
Задача 2.4 Имеется смесь, состоящая из 25% аммиака, а оставшиеся азот и водород находятся в мольном соотношении 1:3. Газ находится при давлении 270 атм и температуре 550 К. Рассчитайте мольный объем смеси, используя уравнения идеального газа, Рейндлиха-Квонга и Соаве-Рейндлиха-Квонга. Сравните результаты. Объясните различия. Является ли газ идеальным?
Скачать задачу 2.4 (моделирование процессов) цена 100р
Задача 2.5 Определите молярный объем метанола при давлении 100 атм и температуре 300 °С, используя уравнение Соаве-Рейндлиха-Квонга. Критические показатели для метанола TС = 512.6 К, РС = 79.9 атм, a = 8.96, b = 0.04561, ω = 0.559. Единицы измерения a и b соответствуют v, измеряемому в л/(г моль). Объясните почему в данном случае не подходят уравнения идеального газа и Рейндлиха-Квонга. Дополнительные сведения: при давлении 9.174 МПа и температуре 300 °С мольный объем метанола составляет 0.373 л/(г моль).
Скачать задачу 2.5 (моделирование процессов) цена 100р
Задача 2.6 Имеется смесь на выходе из реактора для синтеза метанола: СО – 100, Н2 – 200, метанол – 100 кмоль/ч. Газ находится при давлении 100 атм и температуре 300 °С. Рассчитайте мольный объем смеси, используя уравнения идеального газа, Рейндлиха-Квонга и Соаве-Рейндлиха-Квонга. Объясните различие результатов. Почему уравнения идеального газа и РК дают неверные результаты. Ацентрические факторы: СО – 0.049, Н2 – 0.22, метанол – 0.559.
Скачать задачу 2.6 (моделирование процессов) цена 100р
3 Равновесие «пар-жидкость»
Задача №3.1. Провести расчёт сепарационного блока (на рисунке) процесса разделения многокомпонентной углеводородной смеси (рассчитать состав и количество газовых и жидких потоков на выходе из каждого сепаратора) и исследовать влияние технологических параметров на процесс сепарации.
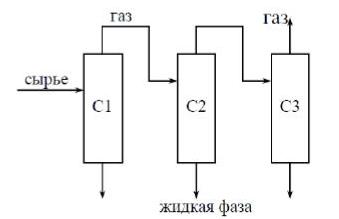
Рис. 3.1 - Принципиальная схема сепарационного блока. С – это сепараторы.
Таблица 3.1. Исходные данные для расчета процесса сепарации
|
Компонент |
Мольная масса |
Мол масса |
Плотность газа, кг/м3 |
Плотность жидкости, кг/м3 |
Темп. кипения, ºС |
Критическая темп-ра, К |
Критическое давление, атм |
|
CO2 |
0,00538 |
4 |
1,9650 |
859 |
-78,2 |
304,2 |
72,83 |
|
N2 |
0,02648 |
28 |
1,2510 |
570 |
-195,8 |
126,2 |
33,5 |
|
CH4 |
0,8486 |
16 |
0,7162 |
300 |
-161,58 |
190,6 |
45,4 |
|
C2H6 |
0,0424 |
30 |
0,3420 |
460 |
-88,7 |
305,4 |
48,2 |
|
C3H8 |
0,2628 |
44 |
1,969 |
501 |
-42,06 |
369,8 |
41,9 |
|
i-C4 |
0,00759 |
58 |
2,5948 |
557 |
-11,73 |
408,1 |
36 |
|
C4 |
0,00548 |
58 |
2,5948 |
580 |
-0,5 |
425,9 |
37,5 |
|
C5 |
0,0083 |
72 |
3,22 |
616 |
36,1 |
469,6 |
33,3 |
|
Остаток |
0,02692 |
108 |
3,88 |
721 |
100,7 |
537,3 |
28 |
|
H2O |
0,00358 |
18 |
0,804 |
1000 |
100 |
647,3 |
217,6 |
|
CH3OH |
0,00085 |
32 |
2,678 |
791 |
64,65 |
512,6 |
79,9 |
Базовые термобарические условия в сепараторах:
P1 = 13,8 МПа, Т1 = 21.8 ºС (сепаратор С1);
P2 = 9,7 МПа, Т2 = 8.6 ºС (сепаратор С2);
P3 = 5,4 МПа, Т3 = 34.8 ºС (сепаратор С3).
После выполнения базового расчёта необходимо исследовать влияние технологических параметров на процесс сепарации согласно своему варианту. Вариант выбирается по последнему числу номера зачётной книжки.
Вариант 0 Исследовать влияние температуры в первом сепараторе
Скачать задачу 3.1 (моделирование процессов) цена 200р
4 Гидродинамические модели
Задача 4.1 (вар 8) Через насадочный аппарат длиной L = 10 м, внутренним диаметром d = 0,065 м и коэффициентом заполнения насадкой ϕ=0,67 протекает жидкость с объемной скоростью v = 0,001 м3/с. Построить математическую модель структуры гидродинамического потока в аппарате.
|
t, c |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
c |
0 |
0,1 |
1,1 |
3,6 |
7,2 |
11,3 |
14,9 |
17,6 |
19,1 |
19,5 |
продолжение таблицы
|
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
29 |
30 |
|
19 |
16 |
12,1 |
8,4 |
5,4 |
3,4 |
2 |
1,2 |
0,6 |
0,8 |
0,5 |
Скачать задачу 4.1 (моделирование процессов) цена 200р
Задача 4.2 Построить ячеечную модель гидродинамики насадочного абсорбера по газовому потоку. Высота насадки 11.5 м, площадь поперечного сечения абсорбционной колонны 1.8 м2, объемная скорость потока 10 000 м3/ч.
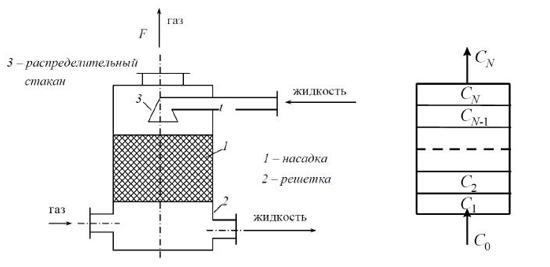
Рис. 4.2. Насадочный абсорбер и его ячеечная схема.
Начальная концентрация абсорбируемого компонента в газовом потоке и экспериментальная кривая абсорбции (зависимость концентрации компонента на выходе из колонны от времени) приведены в таблице 4.2. Вариант выбирается по последнему числу номера зачётной книжки. Необходимо выполнить расчёты при разных значениях числа ячеек ячеечной модели и выбрать оптимальное число ячеек. Сделать вывод.
Начальная концентрация абсорбируемого компонента в % (об.) 0,155
|
Время, с |
вар 0 |
|
0 |
0 |
|
1 |
0,0025 |
|
2 |
0,01 |
|
3 |
0,026 |
|
4 |
0,049 |
|
5 |
0,072 |
|
6 |
0,09 |
|
7 |
0,115 |
|
8 |
0,13 |
|
9 |
0,146 |
|
10 |
0,154 |
Скачать задачу 4.2 (моделирование процессов) цена 200р
Задача 5.1 В теплообменнике типа «труба в трубе» охлаждается жидкость. Хладоагент и охлаждающаяся жидкость движутся прямотоком. Построить математическую модель теплообменного аппарата. Определить температуру теплоносителей на выходе из аппарата. Построить температурные профили по длине аппарата. Исходные данные приведены в таблице 5.1.
Таблица 5.1 – Исходные данные
|
Вариант |
Теплоноситель |
Начальная температура, ºС |
Объёмный расход, м3/с |
Плотность, кг/м3 |
Теплоёмкость, Дж/кг ºС
|
|
10 |
Горячий Холодный |
220 35 |
2,4*10-4 5,5*10-4 |
900 990 |
3.53*103 4.0*103 |
Исследования по длине теплообменника проводятся с целью определения длины, необходимой для завершения процесса теплообмена. Длину теплообменника увеличивают до тех пор, пока процесс теплообмена практически не завершится, т. е. пока разность температур горячего теплоносителя и хладоагента не достигнет 1.5–2 ºС.
Дополнительно нужно исследовать влияние температуры и расхода теплоносителя и хладоагента. Исследования по изменению температуры проводятся с целью изучения влияния температуры хладоагента на расход хладоагента. После изменения температуры хладоагента изменяют расход хладоагента до тех пор, пока конечные температуры горячего теплоносителя и хладоагента не достигнут требуемых значений.
Скачать задачу 5.1 (моделирование процессов) цена 200р


