Решебник 4
4.1 Решение задач маш гидравлика 1
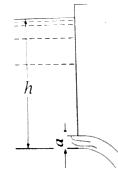
Задача 1-1. Определить полное гидростатическое давление на дно сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде h =0,60 м.
Расчет выполнить: 1) в системе МКГСС, 2) в международной системе единиц (СИ), 3) во внесистемных механических единицах.
Скачать решение задачи 1.1 (Решебник 4) (цена 60р)
Задача 1-3. Определить высоту столба воды в пьезометре над уровнем жидкости в закрытом сосуде. Вода в сосуде находится под абсолютным давлением Р1 = 1,06 ат (рис. 1-10),
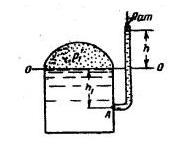
Скачать решение задачи 1.3 (Решебник 4) (цена 60р)
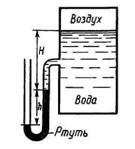
Задача 1-5. Определить высоту, на которую поднимается вода в вакуумметре, если абсолютное давление воздуха внутри баллона Рн=0,95 ат (рис. 1-11). Сформулировать, какое давление измеряет вакуумметр.
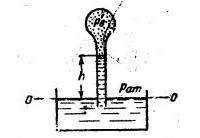
Скачать решение задачи 1.5 (Решебник 4) (цена 60р)
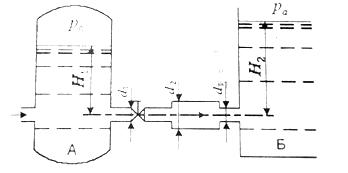
Задача 1-9. Определить манометрическое давление в точке А трубопровода, если высота столба ртути по пьезометру h2=25см Центр трубопровода расположен на h1 = 40 см ниже линии раздела между водой и ртутью (рис. 1-13).
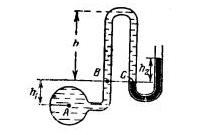
Скачать решение задачи 1.9 (Решебник 4) (цена 60р)
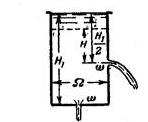
Задача 1-13. В цилиндрический сосуд при закрытом кране В и открытом кране Л наливается ртуть при атмосферном давлении до высоты h1 = 50 см. Высота сосуда Н = 70см. Затем кран А закрывается, а кран В открывается. Ртуть начинает вытекать из сосуда в атмосферу. Предполагая, что процесс происходит изотермически, определить вакуум в сосуде при «овом положе-нии уровня h2 в момент равновесия (рис, 1-16) и величину h2.
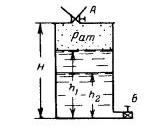
Скачать решение задачи 1.13 (Решебник 4) (цена 60р)
Задача 1.14 В сосуд М, соединенный с сосудом N (рис.1-17), при закрытом кране В наливается ртуть при атмосферном давлении до высоты h = 60 см. Затем кран А закрывается, кран В открывается. Ртуть из сосуда М начинает выливаться открытый сосуд N, сообщающийся с атмосферой. Определить: 1) на какую высоту h1 опустится уровень в сосуде М при установлении равновесия, если площадь поперечного сечения левого сосуда S1 = 2700 см2 а правого S2= 300 см2? Высота сосуда H = 90 см.
2) На какую высоту h2 поднимется ртуть в правом сосуде?
3) Чему будет равно абсолютное давление в сосуде? Принять, что процесс изотермический.
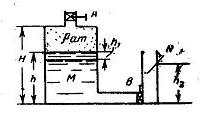
Скачать решение задачи 1.14 (Решебник 4) (цена 150р)
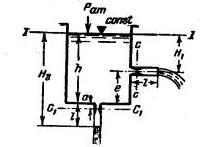
Задача 1.15 К дну резервуара присоединен U-образный пьезометр, один конец которого открыт и сообщается с атмосферой (рис. 1-18). В резервуар по трубопроводу М нагнетается масло (γм = 7358 H/м3 = 750 кг/м3).
Считая, что в начальный момент давление в резервуаре было атмосферным, определить высоту столба жидкости h в резервуаре, если ртуть в левой трубке пьезометра; поднялась на z = 40,15 см по сравнению с первоначальным положением, а в правой опустилась на ту же величину, уступив место жидкости. Высота резервуара H = 1,5м. Процесс считать изотермическим.
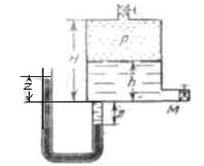
Скачать решение задачи 1.15 (Решебник 4) (цена 150р)
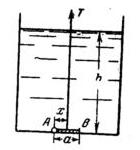
Задача 1.16 Определить при помощи дифференциального манометра разность давлений в точках В и А двух трубопроводов, заполненных водой. Высота столба ртути =20 см. Удельный вес ртути 133416 Н/м3 13600 кг/м3, воды 9810 Н/м3.
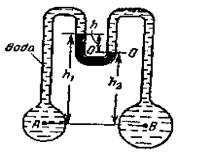
Скачать решение задачи 1.16 (Решебник 4) (цена 60р)
Задача 1-18. Определить при помощи дифференциального манометра разность давлений в точках В и А двух трубопроводов, заполненных водой. Высота столба ртути h1-h2=h = 20 см. Удельный вес ртути - 133416 н/м3 = 13600 кГ/м3, воды - 9810 н/м3 (рис. 1-19).
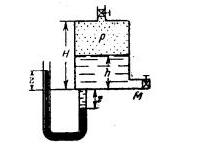
Скачать решение задачи 1.18 (Решебник 4) (цена 60р)
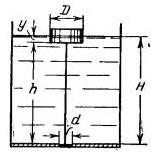
Задача 1-25. Глубина воды в цилиндрическом сосуде диаметром D = 60 см равна hн = 80 см. Определить .полное гидростатическое давление при вращении сосуда (n = 90 об/мин) для точек а, b, с и d., отстоящих на расстоянии z =40 см от дна сосуда (рис. 1-22) и расположенных на окружности с радиусом соответственно r1 = 0, r2= 10 см, r3 =20 см и r4=r0 = 30 см.
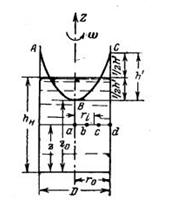
Скачать решение задачи 1.25 (Решебник 4) (цена 60р)
Задача 1-28. Построить поверхности равного давления (рис. 1-23) P'=Pат=98100 Н/м3=1 кГ/см2, Р' = 100062 Н/м3 = 1,02 кГ/см2, Р'= 102024 Н/м3=1,04 кГ/см2, Р'=103986Н/м2=1,06 кГ/см2 в вертикальной плоскости, проведенной по диаметру цилиндрического сосуда, который наполнен водой и вращается с постоянной угловой скоростью w=8,1 1/сек. Вычислить координаты этих поверхностей для вертикалей, проведенных через точки, расположенные на окружности радиуса соответственно r1 = 10 см, r2 = 20 см и r3=30 см. Известно, что при вращении наинизшая точка свободной поверхности расположена на расстоянии rо=0,6 м. Диаметр сосуда d =0,6 м. Сосуд сверху открыт. Проверить величину давления в точке А (r2=20 см, z=zА = 53,36 см).
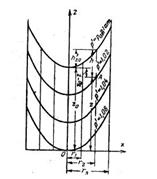
Скачать решение задачи 1.28 (Решебник 4) (цена 60р)
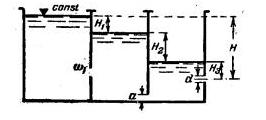
Задача 1-31. Определить силу манометрического давления на дно сосудов а, б, в и г (рис. 1-24), наполненных водой. Высота столба h= 60 см, а h1=50 см и h2 = 40 см. Площадь дна сосудов w = 1250 см2, а площадь сечения w1= 12,50 см2. Найти силу, передаваемую в каждом случае на пол, пренебрегая весом сосуда. Почему сила давления на дно не всегда совпадает с весом воды, заключенной ,в сосуде? Объясните гидростатический парадокс, определив силу •манометрического давления, воспринимаемую фасонной частью АВСD (б) или АВ (схемы в и г).
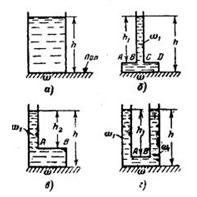
Скачать решение задачи 1.31 (Решебник 4) (цена 60р)
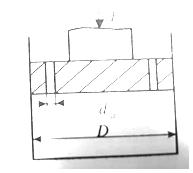
Задача 1-33. Определить силу манометрического давления иа дно сосуда, если сила P1, действующая на поршень, равна 44 H (рис. 1-26). Диаметр d=12 см, глубина воды в сосуде h=40 см, диаметр дна сосуда D=35 см.
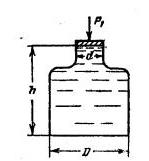
Скачать решение задачи 1.33 (Решебник 4) (цена 60р)
Задача 1-42. Определить силу давления воды, приходящуюся н« 1 л ширины плоского затвора и центр давления. Дано: h1=5м, h2=1,2 м, h=3 м. Угол наклона затвора к горизонту а=45°. Давление на свободную поверхность с обеих сторон затвора атмосферное (рис. 1-36),
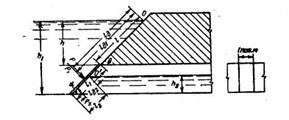
Скачать решение задачи 1.42 (Решебник 4) (цена 60р)
Задача 1-43. Глубина воды перед вертикальным затвором h=6 м (рис. 1-37). Требуется расположить четыре горизонтальных ригеля (двутавровые балки) так, чтобы на каждый ригель приходилась одинаковая сила давления воды Pi которая передается на ригели через обшивку плоского затвора. Расчет произвести на I м ширины затвора. Задачу решить графо-аналитическим способом, а расстояние, измеренное по чертежу, от свободной поверхности до каждого ригеля проверить аналитически по формуле (1-11).
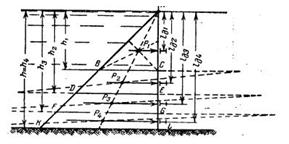
Скачать решение задачи 1.43 (Решебник 4) (цена 60р)
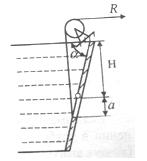
Задача 1-45. Найти силу Т, с которой .нужно тянуть трос, прикрепленный к нижней кромке плоского круглого затвора диаметром d=2 м, закрывающего отверстие трубы. Затвор может вращаться вокруг шарнира A. Глубина воды над верхней кромкой затвора h=3 м (.рис. 1-39). Трос направлен под углом 45° к горизонту.
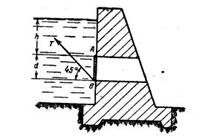
Скачать решение задачи 1.45 (Решебник 4) (цена 60р)
Задача 1-47. Прямоугольный плоский затвор шириной b = 2 м вверху поддерживается крюками, а внизу соединен шарнирно по горизонтальной оси с дном сооружения. В верхнем бьефе глубина воды h1=3 м, а=0,5 м (рис. 1-41). Определить реакцию в шарнире Ra и реакции крюков Rb от давления жидкости в двух случаях: 1) в нижнем бьефе воды нет; 2) глубина воды в нижнем бьефе равна 1,5 м.
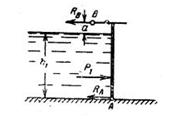
Скачать решение задачи 1.47 (Решебник 4) (цена 60р)
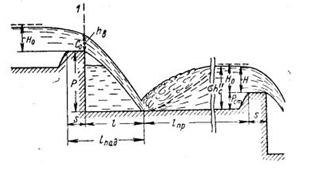
Задача 1-68. Прямоугольный канал шириной b=7 м перекрывается сегментным затвором. Глубина воды в канале перед затвором А, =4,80 м, в нижнем бьефе hи=2 м. Радиус затвора r=7,5 м. Ось вращения затвора расположена на h = 1 л выше горизонта воды перед затвором (рис. 1-55). Определить: 1) Силу давления воды на затвор слева и координаты ее центра давления. Проверить вычисленные координаты графически. 2) Силу давления воды на затвор справа и координаты ее центра давления. Проверить вычисленные координаты графически. 3) Равнодействующую силу давления воды на затвор и координаты ее центра давления. 4) Подъемное усилие Т, предполагая, что вес затвора G приложен в середине пролета на биссектрисе угла а на расстоянии 0,75- от оси вращения О-О'. При расчете трением в шарнире пренебречь. Вес затвора определить по формуле А. Р. Береэинского
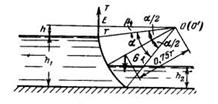
Скачать решение задачи 1.68 (Решебник 4) (цена 60р)
Задача 1-69. Определить силу манометрического давления воды на цилиндрический затвор, перегораживающий прямоугольный канал, и центр давления, если глубина перед затвором h1 = 4,2 м, диаметр затвора d=3м, а ширина пролета b=10 м. Воды в нижнем бьефе.
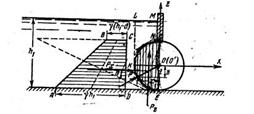
Скачать решение задачи 1.69 (Решебник 4) (цена 60р)
Задача 1-70. Цилиндрический затвор может вращаться вокруг горизонтальной оси (рис. 1-58). Центр тяжести затвора находится на радиусе, расположенном под углом ф=45° « горизонту, и удален от оси вращения на ОА =1/5r. Радиус затвора r=40 см, ширина b=100 см. Глубина воды h. Определить Необходимый вес затвора, чтобы затвор находился в равновесии и занимал положение, указанное на рис. 1-58.
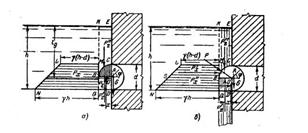
Скачать решение задачи 1.70 (Решебник 4) (цена 60р)
Задача 1-86. Определить величину сжимающего усилия Р2. производимого одним рабочим у гидравлического пресса, если большое плечо рычага имеет длину a=1 м, а малое b=0,1 м, диаметр поршня пресса D=250 мм, диаметр поршня насоса d=25 мм, усилие одного рабочего Р=147H= 15 кГ. Коэффициент полезного действия 0,85 (рис. 1-71).
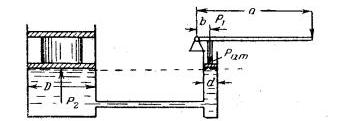
Скачать решение задачи 1.86 (Решебник 4) (цена 60р)
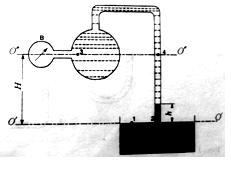
Задача 1-88. Определить давление, создаваемое гидравлическим грузовым аккумулятором (рис. 1-72) и запасаемую им энергию при следующих данных: вес движущихся частей G=725940 H=74000 кГ, диаметр плунжера d=20 см, площадь поперечного сечения плунжера w=314см2, ход плунжера H=6 м. Коэффициент полезного действия аккумулятора 0,85.
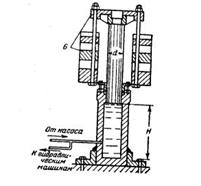
Скачать решение задачи 1.88 (Решебник 4) (цена 60р)
Задача 1-93, Определить вес поплавка диаметром D=20 см, который при слое бензина H ≥ 80 см обеспечивал бы автоматическое открытие клапана диаметром d = 4 см (рис. 1-76). Длина тяги h = 74 см. Вес клапана и тяги принять 1,7 H = 0,173 кг. Относительный удельный вес бензина 0,75.
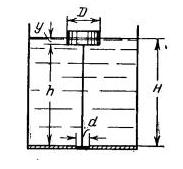
Скачать решение задачи 1.93 (Решебник 4) (цена 60р)
Задача 1-104. Проверить остойчивость плавания на воде совершенно одинаковых по своим размерам брусьев квадратного поперечного сечения, выполненных из однородных материалов со следующими относительными удельными весами: 1) дуб (т) =0,9, 2) бук (т) =0,80, 3) береза (т)=0,75, 4) соcна (т)=0,50, 5) пробковое дерево (т) =0,25, 6) особо легкий материал (n)=0,125.
Скачать решение задачи 1.104 (Решебник 4) (цена 60р)
Задача 1-105. Определить остойчивость треугольной равнобедренной призмы, имеющей следующие размеры: ширина поверху b = 1,4 м. Длина l = 5 м. Угол при вершине а=60°. Относительный удельный вес призмы 0,75 (рис. 1-79).
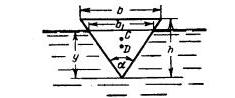
Скачать решение задачи 1.105 (Решебник 4) (цена 60р)
Задача 1-106. Определить остойчивость металлической баржи (рис. 1-80) в порожнем и груженом состоянии. После загрузки возвышение ее борта над водой 0,5 м. Ширина баржи b=8 м, клипа l=60 м, высота h = 3,50 м, толщина стенок δ = 0,01 м, груз - мокрый песок (относительный удельный вес 2,0). Относительный удельный вес железа 7,8. Для упрощения расчета принять, что 1) баржа имеет прямоугольное очертание, 2) вес переборок и других конструктивных частей баржи условно отнесен к весу ее стенок.
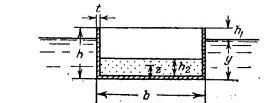
Скачать решение задачи 1.106 (Решебник 4) (цена 60р)
Задача 2.10 Горизонтальное сопло запроектировано таким образом, что скорость воды вдоль осевой линии изменяется по линейному закону от «1=2 м/сек до u1=20 м/сек на длине 40 см (рис. 2-9,а). Определить разность давлений, соответствующую этому изменению скорости, пренебрегая потерями на трение. Вычислить величину градиента давления в начальном сечении и в конечном, отстоящем от него на 40 см. Построить эпюру изменения пьезометр метрического напора z+P/y - по оси сопла, считая, что давление в конечном сечении равно атмосферному.
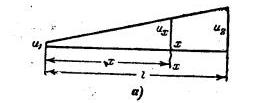
Скачать решение задачи 2.10 (Решебник 4) (цена 60р)
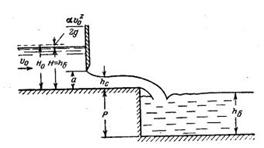
Задача 2-32. Определить глубину Воды hг во входной части сооружения прямоугольного сечения и ширину bг (рис. 2-17), чтобы отношение площади живого сечения после сужения к площади живого сечения в канале составляло 0,4. Расчетный расход Q= 10 ч3/сек. Канал трапецеидального сечения с коэффициентом заложения откоса m=ctdO=1,5 и шириной по дну b1 = 6 м. Глубина воды в канале h1 = 1,5 м. высота порога при входе Р=0,3 м. Построить линию удельной энергии и показать пьезометрическую линию.
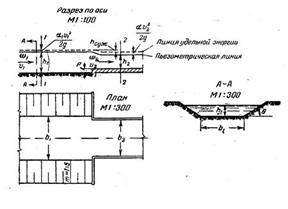
Скачать решение задачи 2.32 (Решебник 4) (цена 60р)
Задача 2-34. Вода при температуре t=12 °С подается по трубе диаметром d = 4 см. Расход воды Q=70 см3/сек. Определить режимы потока и описать характер движения струйки краски, введенной в центре поперечного сечения трубы. Какой расход нужно пропускать по трубе, чтобы изменить режим движения?
Скачать решение задачи 2.34 (Решебник 4) (цена 60р)
Задача 2-40. Вычислить коэффициент Кориолиса при ламинарном движении и выразить среднюю скорость v через максимальную umax при условии, что скорость в открытом прямоугольном лотке глубиной h (рис. 2-19) и шириной b изменяется от нуля у дна до максимальной на поверхности по уравнению параболы
Скачать решение задачи 2.40 (Решебник 4) (цена 60р)
Задача 2-43. Определить потери напора в водопроводе длиной l = 500 м при подаче Q =100 л/сек, если трубы чугунные, бывшие в эксплуатации, d = 250 мм и шероховатость 1,35 мм. Температура воды t = 10 °С
Скачать решение задачи 2.43 (Решебник 4) (цена 60р)
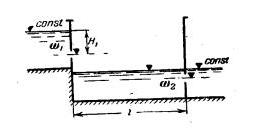
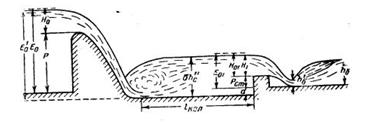
Задача 2-45. Определить, какой расход можно перекачать сифоном из водоема А в водоем В при разности горизонтов H = 1,5 м (рис. 2-20), если длина сифона l=75 м, а диаметр сифона d=200 мм. Трубы чугунные, нормальные (шероховатость 1,35 мм). Вычислениями выяснить, будет ли в сечениях 1-1, 2-2, 3-3, 4-4, 5-5 манометрическое давление или вакуум? Найти, где расположены сечения, в которых давление в сифоне будет равно атмосферному. Почему в сечении 3-3 будет наибольший вакуум? При расчете скоростными напорами в водоемах пренебречь. Наибольшее превышение над уровнем воды в водоеме л принять s=2 м, а глубины погружения h1 = 2 л и h2=1 м. Температура воды t=15°С.
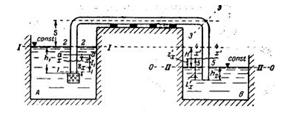
Скачать решение задачи 2.45 (Решебник 4) (цена 60р)
4.1 Решение задач маш гидравлика 2
Задача 2-51. Для отвода воды необходимо под проезжей частью дороги проложить железобетонный дюкер (рис. 2-24). Определить диаметр дюкера, который обеспечил бы пропуск расхода Q=0,95 м3/сек при разности горизонтов H=0,20 м. Длина дюкера l=15 м, угол поворота а=30°. Скорость в верхнем канале v1 =0,7 м/сек, в нижнем v2=0,8 м/сек. Температуру воды принять t=20° С. Высота шероховатости стенок дюкера 1 мм.
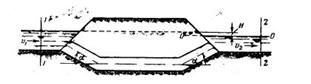
Скачать решение задачи 2.51 (Решебник 4) (цена 60р)
Задача 2-53. В канале трапецеидального сечения с шириной по дну b=8,50 м глубина воды при равномерном движении h = 1,7 м. Расход Q=15 м3/сек. Определить потерн напора на участке длиной l=1 км, пользуясь различными формулами. При расчетах принять коэффициент заложения откосов канала m=1. Канал в средних условиях содержания и ремонта.
Скачать решение задачи 2.53 (Решебник 4) (цена 60р)
Задача 3-8. Через цилиндрический насадок, расположенный в стенке (рис. 3-10), расходуется вода в количестве Q=5,6 л/сек. Диаметр насадка d =3,8 км, длина l= 15 см. Определить напор Н над центром насадка, скорость Во и давление рс а насадке (в сжатом сечении).

Скачать решение задачи 3.8 (Решебник 4) (цена 60р)
Задача 3-9. Сравнить пропускную способность и скорость истечения из отверстия и насадков, показанных на рис. 3-2, при условии, что напор над центром выходного сечения во всех случаях одинаковый: H=2,0 м. Диаметр выходного сечения d всех насадков, кроме расходящегося, принять равным 5 см. Длина насадков l=20 см.

Скачать решение задачи 3.9 (Решебник 4) (цена 60р)
Задача 3-13. Резервуар разделен на три отсека перегородками, в которых имеются отверстия (рис. 3-13): в первой перегородке прямоугольное с площадью w1=8,5 см2, во второй перегородке - квадратное, примыкающее одной стороной а = 4 см к дну. В наружной стенке отверстие круглое d=3,0 см. Разность между отметкой уровня воды в левом отсеке и отметкой центра наружного отверстия H=3,10 м.
Скачать решение задачи 3.13 (Решебник 4) (цена 60р)
Задача 3-14. Определить расход из большого резервуара через два цилиндрических насадка и величину вакуума в них. Один насадок расположен горизонтально в боковой стенке резервуара на расстоянии е=20 см от дна, яругой - вертикально в дне резервуара (рис. 3-14). Размеры насадков одинаковы: d=6 см, l=20 см. Глубина воды в резервуаре h=100 см.
Скачать решение задачи 3.14 (Решебник 4) (цена 60р)
Задача 3-15. В теле железобетонной плотины проектируется водоспуск в виде трубы длиной l=5,0 м (рис. 3-15). Напор над водоспуском при свободном истечении равен H1 = 6,5 м. Разность отметок уровней воды в верхнем и нижнем бьефах плотины H2=15,0 м. Скорость подхода воды к плотине v0=0,40 м/сек. Определить диаметр d водоспуска, если расход Q=12,0 м3/сек. Кроме того, установить: а) какой будет расход Q1 через водоспуск, если уровень нижнего бьефа поднимется на 10 м;
Скачать решение задачи 3.15 (Решебник 4) (цена 60р)
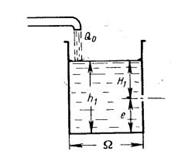
Задача 3.18. Из резервуара с площадью поперечного сечения S1=5,0м2 Ω1 = 5м2 через отверстие в стенке вода поступает в смежный резервуар, имеющий площадь S2=3,5м2 Ω2 = 3,5м2. Отверстие w = 80см2 расположено на высоте е=1,2м от дна. Через какое время t после открытия отверстия из первого резервуара во второй вытечет вода в количестве 7,5м2, если в момент открытия отверстия глубина в первом резервуаре была h1 = 3,8м, а второй был пуст. Притока в резервуары извне нет.
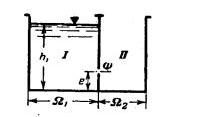
Скачать решение задачи 3.18 (Решебник 4) (цена 60р)
Задача 3-19. Через какое время t после открытия отверстия (рис. 3-17) из первого резервуара во второй вытечет вода в количестве 7,50 м3 в условиях предыдущей задачи.

Скачать решение задачи 3.19 (Решебник 4) (цена 60р)
Задача 3-25. Цилиндрический бак с площадью S=3,0 м2 и высотой H1=4,0 м, заполненный до краев водой, нужно опорожнить за время t = 5,0 мин. Определить необходимую для этого площадь двух одинаковых отверстий, одно из которых расположено в центре дна, другое в стенке, на половине высоты бака (рис. 3-21).
Скачать решение задачи 3.25 (Решебник 4) (цена 60р)
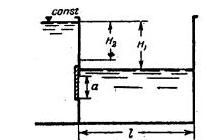
Задача 3-27. Цилиндрический резервуар имеет площадь поперечного сечения S = 1,2 м2. В его стенке на расстоянии е=30 см от дна расположено круглое отверстие d=3 см (рис. 3-23). Постоянный приток воды в резервуар Q0=2,5 л/сек. Определить глубину воды h2 в резервуаре через 20 мин после открытия отверстия, если в момент его открытия глубина h1=1,50 м.
Скачать решение задачи 3.27 (Решебник 4) (цена 60р)
Задача 3-31. Щитовое отверстие имеет ширину b= 1,5 м и высоту а=1,0 м. Щит приподнимается равномерно со скоростью v =2,5 см/сек (рис. 3-26). Определить объем воды W, вытекающий за время t=40 сек полного открытия отверстия. Напор над центром отверстия H1=3,5 м. Истечение свободное. Коэффициент расхода отверстия 0,6=const.
Скачать решение задачи 3.31 (Решебник 4) (цена 60р)
Задача 3-32. Определить время t наполнения шлюзовой камеры до уровня верхнего бьефа, если разность уровней в верхнем бьефе и в камере составляет H1=9,0 м (рис. 3-27). Длина камеры l=40 м, ширина bк=12,0 м. Отверстие, через которое заполняется камера, имеет ширину b = 1,0 м, высоту a=0,5 м. При расчете учесть расход через отверстие за время его открытия, если скорость подъема затвора v=1,0 см/сек. Коэффициент расхода отверстия принять 0,6=const.
Скачать решение задачи 3.32 (Решебник 4) (цена 60р)
Задача 3-33. Определить количество времени t на шлюзование парохода из верхнего бьефа в нижний при следующих условиях (рис. 3-28): длина шлюзовой камеры l=50 м, ширина b=12 м. Размеры верхнего и нижнего водоспускных отверстий: высота а= 1,0 м, ширина b=1,5 м (w1=w2=1,5 м2), м=0,70. Скорость подъема затворов v=1,0 см/сек.
Высотные отметки: уровня верхнего бьефа (УВБ) 41,0 л; уровня нижнего бьефа (УНБ) и уровня воды в камере 33,0 м; центра верхнего отверстия 38,0 м; нижнее отверстие заглублено под уровень НБ. На открытие шлюзовых ворот и передвижку парохода затрачивается время t0=10 мин. Задачу решить в двух вариантах: а) без учета времени, затрачиваемого на открытие отверстий; б) с учетом времени, затрачиваемого на открытие отверстий, в течение которого расход изменяется в зависимости от площади отверстия и от напора.
Скачать решение задачи 3.33 (Решебник 4) (цена 60р)
Задача 3-35. Определить скорость v равномерного подъема затвора, при которой объем воды, вытекший из отверстия за время его открытия, составляет 5% заполняемого водой объема камеры (рис. 3-27). Размеры камеры: lk=80 м, bк = 18,0 м, размеры отверстия а=0,8 м, b=3,0 м, μ=0,70. Напор H=8,0 м.
Скачать решение задачи 3.35 (Решебник 4) (цена 60р)
Задача 3-36. Определить скорость V равномерного подъема затвора, открывающего отверстие в шлюзовой камере, при которой период 1\ полного открытия отверстия составит 10% времени наполнения камеры до отметки верхнего бьефа (рис. 3-27). Размеры камеры: lк=30 ж, bk = 12.0 м, напор H1 = 5,0 м. Размеры отверстия: высота а=0,75 м, ширина b = 1,5 м, м=0,60.
Скачать решение задачи 3.36 (Решебник 4) (цена 60р)
Задача 3-38. Двухкамерный шлюз (рис. 3-29) имеет размеры камер: ширину b = 10,0 м, длину l = 55 м. Отметки: уровня верхнего бьефа 20,0 м; центра верхнего отверстия 18,0 м; уровня воды в верхней камере 15,0 м; центра среднего отверстия 11,5 м; уровня воды в нижнем бьефе и нижней камере 9,2 м; центра нижнего отверстия 7,5 м. Определить площадь водопропускных отверстий (о при условии, чтобы время шлюзования парохода из верхнего бьефа в нижний Т равнялось 25 мин, из которых tо=10 мин, затрачиваются на открытие ворот и передвижение парохода. Коэффициент расхода принять 0,70. Время «а открытие отверстий не учитывать.
Скачать решение задачи 3.37 (Решебник 4) (цена 60р)
Задача 3-41. Определить время t опорожнения цилиндрического резервуара, заполненного водой, имеющего диаметр d=2,4 м и высоту l = 6,0 м в двух случаях (рис. 3-31). а) Резервуар поставлен вертикально. Отверстие w = 1,76 дц2 расположено в дне. б) Резервуар лежит горизонтально. Отверстие w = 1,76 дц2 расположено на боковой поверхности внизу. В обоих случаях при истечении обеспечен доступ воздуха в резервуар.
Скачать решение задачи 3.41 (Решебник 4) (цена 60р)
Задача 3-42. Сосуд, имеющий форму усеченного конуса, поставлен вертикально на меньшее основание с диаметром D (рис. 3-32). Определить (в общем виде) время t опорожнения сосуда через отверстие ад, расположенное в основании.
Скачать решение задачи 3.42 (Решебник 4) (цена 60р)
Задача 3-43. Определить в общем виде время t изменения напоров воды от H1 до H2 при истечении из резервуара, имеющего форму усеченной пирамиды с прямоугольными основаниями (рис. 3-33). Отверстие и расположено в нижнем (меньшем) основании. Углы наклона граней резервуара к горизонту Q и ф.
Скачать решение задачи 3.43 (Решебник 4) (цена 60р)
Задача 3-44. На рис. 3-34 показана плотина, и на рис. 3-35 план водохранилища перед ней с горизонталями через 1м и график зависимости площади зеркала водохранилища от его глубины. В водохранилище из реки выступает постоянный расход Qо=4,16 м3/сек. Определить время опорожнения водохранилища от отметки 36,0 до отметки 31,0 м, если площадь водоспуска в плотине, через который свободно вытекает вода из водохранилища, составляет w=11,0 м3. Центр водоспуска расположен на отметке 30,0 м. Коэффициент расхода принять 0,7.
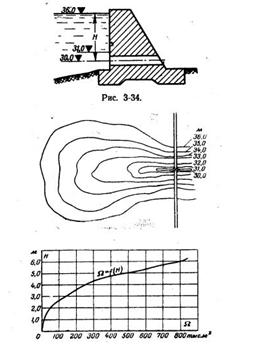
Скачать решение задачи 3.44 (Решебник 4) (цена 60р)
Задача 3-45. Определить площадь w водовыпускного отверстия в водохранилищной плотине, чтобы опорожнить водохранилище за 1 сутки. На рис. 3-36 представлен план водохранилища в горизонталях и построенный по этому плану график зависимости площади зеркала S от отметок z зеркала водохранилища. Притока воды в водохранилище нет. Центр водовыпускного отверстия расположен на отметке 20,0 м. Коэффициент расхода отверстия принять 0,7.
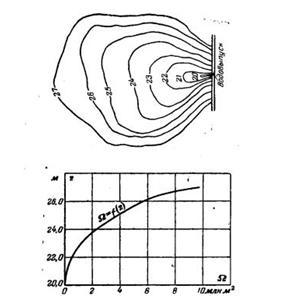
Скачать решение задачи 3.45 (Решебник 4) (цена 60р)
Задача 4-1. Определить расход Q и скорость в трубопроводе, имеющем диаметр d=250 мм и длину l=180 м, если в напорном баке А отметка горизонта воды 12,0 лив конечном пункте В отметка пьезометрической линии 7,2 м (рис. 4-9). Дать расчет для двух случаев: в) трубы металлические, нормальные и б) трубы загрязненные, n=0,015.
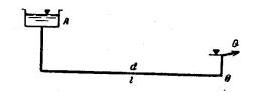
Скачать решение задачи 4.1 (Решебник 4) (цена 60р)
Задача 4-4. Из напорного бака А с отметкой горизонта воды 15,50 м требуется подать в пункт В воду на отметку 10,6 м в количестве Q = 20,6 л/с. Между пунктами А и В расстояние l = 880 м. Для прокладки водопровода имеются «нормальнее» трубы.
Скачать решение задачи 4.4 (Решебник 4) (цена 60р)
Задача 4-14. От напорного бака А в пункт В проложены два параллельных трубопровода (рис. 4-17). В одном из трубопроводов расход распределяется в виде непрерывной раздачи Qнр = 23,0 л/сек. В пункт В поступает транзитный расход Qв на отметку 14,5 м. Горизонт воды в напорном баке А расположен на отметке 21,2 м. Трубы нормальные. Определить: 1) Транзитный расход Qв в пункте В. 2) Отметку горизонта воды в напорном баке Л, обеспечивающую увеличение расхода ^в в 2 раза (при этом расход Qп.р и отметка пьезометрической линии в пункте В остаются без изменения).
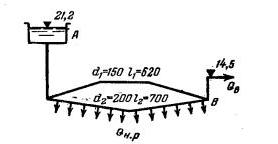
Скачать решение задачи 4.14 (Решебник 4) (цена 60р)
Задача 4-20. Через систему труб, состоящую из трех последовательно соединенных участков подводится вода от напорного бака А к потребителям (рис. 4-23). На участках АВ и ВС вода расходуется в виде непрерывной раздачи. По трубе СD идет до конца транзитный расход Q0. Размеры труб, отметки и расходы показаны на рисунке. Трубы нормальные. Определить: 1) Отметку Н0 пьезометрической линии в конечном пункте В. 2) Какой диаметр Л дополнительного параллельного АВ трубопровода (показан на рисунке пунктиром), потребуется взять, чтобы отметка пьезометрической линии в пункте D повысилась на 1,5 м?
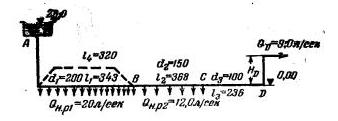
Скачать решение задачи 4.20 (Решебник 4) (цена 60р)
Задача 4-22. Два резервуара соединены трубопроводом АСВ (рис. 4-25). В точке С трубопровода поставлен водовыпускной кран. Определить расходы QА и Qв воды из резервуаров при различных расходах воды в точке С от Qс =0 при закрытом кране до QCmax при полном открытии крана. Построить пьезометрическую линию. Размеры труб и отметки уровней воды в резервуарах указаны на схеме. Трубы нормальные.
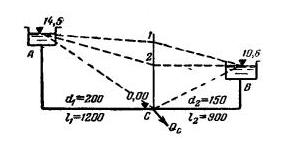
Скачать решение задачи 4.22 (Решебник 4) (цена 60р)
Задача 4-27. Определить расход воды из резервуаров А и Д показанных на схеме (рис. 4-28), если потребление в пунктах В и С составляет соответственно Qн = 12,0 л/сек я Qс = 18,0 л/сек. Построить пьезометрическую линию. Трубы нормальные. Размеры труб и отметки горизонтов воды в резервуарах приведены на схеме.
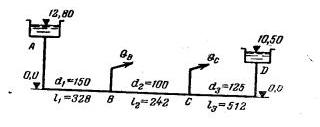
Скачать решение задачи 4.27 (Решебник 4) (цена 60р)
Задача 4-33. Определить диаметры труб на участках замкнутой водопроводной сети, схема которой показана на рис. 4-33. Напор в начальной точке 4 равен H=35,0 я. В пунктах водоразбора должен быть обеспечен остаточный напор Hост=6,0 л. Трубы нормальные. На схеме показаны расходы в литрах в секунду, длины участков труб в метрах, отметки заложения труб в метрах.
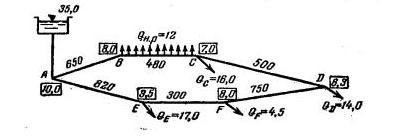
Скачать решение задачи 4.33 (Решебник 4) (цена 60р)
4.1 Решение задач маш гидравлика 3 Насосная станция
Задача 4-35. Нагнетательный трубопровод от насосной станции до напорного резервуара имеет длину l = 430 м. Расход трубопровода Q=68,0 л/сек. Определить экономически наивыгоднейший диаметр и трубопровода при следующих условиях. Стоимость 1 т труб 40 руб. Трубы чугунные, нормальные. Ежегодная доля погашения капитальных затрат на трубопровод р=0,08 (т. е. срок службы трубопровода 12,5 лет).
Стоимость 1 квт-ч энергии 2 коп. Насосная станция работает 20 ч в сутки, 350 дней в году. Коэффициент полезного действия насосной установки 0,75.
Скачать решение задачи 4.35 (Решебник 4) (цена 60р)
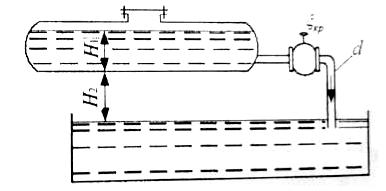
Задача 4-38. Насосная станция подает воду из водохранилища в водонапорную башню. Из водонапорной башни вода поступает в распределительную сеть (рис. 4-36). Рассчитать всасывающую линию, нагнетательную линию, распределительную сеть и мощность насосной установки при следующих условиях:
1) Длины участков труб и отметки заложения их даны на схеме (рис. 4-36,6). Трубы нормальные.
2) Остаточный напор в концевых точках распределительной сети Hoст>8,0 м. 3) Стоимость 1т нагнетательной трубы в деле s=30 руб. Период эксплуатации трубы 15 лет (р=0,067).
4) Стоимость 1 квт*ч энергии «=2,5 коп.
5) Продолжительность работы насосов 350дней в год при 20 ч в сутки.
6) Коэффициент полезного действия насосной установки 0,85.
7) Вакуум насоса Рвак=6,0 м.
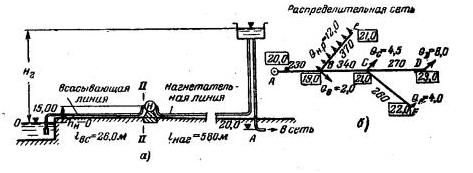
Скачать решение задачи 4.38 (Решебник 4) (цена 60р)
Задача 4-39. Определить повышение давления в трубопроводе Дрмакс и напряжение в его стенках при мгновенном закрытии затвора. Построить график изменения давления у затвора и в сечении 1-1, находящемся на расстоянии 500 м от затвора, а также график изменения скорости »о в сечении 1-1. Начальное манометрическое давление в трубопроводе у затвора Ро=1.5 ат Расход воды в трубопроводе Q=145 л/сек. Диаметр D=300 мм, е=4 мм. Длина l=850 м. Трубопровод стальной Е=2-1011 кГ/м2
Скачать решение задачи 4.39 (Решебник 4) (цена 60р)
Задача 5-1. Определить расход и среднюю скорость в трапецеидальном земляном канале при b=10 м; h=3,5 м; m=1,25; i=0,0002. Грунты лессовые среднеплотные. Канал в средних условиях содержания и ремонта.
Скачать решение задачи 5.1 (Решебник 4) (цена 60р)
Задача 5-6. Определить расход и среднюю скорость в земляном канале параболического сечения при h = 2,1м, P = 4 м; i = 0,0004. Канал в хороших условиях содержания и ремонта. Продольный разрез по оси канала приводится на рис. 5-4.
Скачать решение задачи 5.6 (Решебник 4) (цена 60р)
Задача 5-11. Определить расход в бетонированном канале кругового сечения при h=1 м; r=1,2 м я падении дна 6 см на 1 км длины канала.
Скачать решение задачи 5.11 (Решебник 4) (цена 60р)
Задача 5-14. Определить уклон лотка с r = 0,5 м, при котором расход Q = 0,5 м3/с проходит при глубине h = 0,4 м, если n = 0,014.
Скачать решение задачи 5.14 (Решебник 4) (цена 60р)
Задача 5-15. Определить расход и среднюю скорость в круглой трубе при следующих данных: d=3 м, h=2,10 м; n=0,917; i=0,0009.
Скачать решение задачи 5.15 (Решебник 4) (цена 60р)
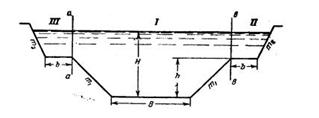
Задача 5-23. Определить расход, который пропускает земляное русло, состоящее из главного русла и двусторонней поймы (рис. 5-5) при следующих данных: В = 50 м; b=25 м; m1= 3; m2 = 2; h= 2,5 м;Р=.4,0 м; nр = 0,025; nn=0,040; 1 = 0,0004.
Скачать решение задачи 5.23 (Решебник 4) (цена 60р)
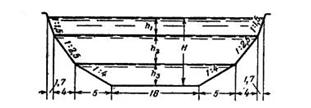
Задача 5-24. Судоходный оросительный канал имеет поперечное сечение, изображенное на рис. 5-6 (размеры в метрах). Откосы 1 : 1,5 и 1 : 2,5 укреплены каменным мощением (n = 0,015), а откосы 1:4 и дно не облицованы (n = 0,0225). Определить необходимый уклон дна канала для пропуска расхода Q =60 м3/сек при глубине наполнения Н.
Скачать решение задачи 5.24 (Решебник 4) (цена 60р)
Задача 5-33. Определить минимальную скорость, допустимую в канале с i=0,00027; n=0,025, если мутность воды достигает р=1,5 кг/м3, а средневзвешенная гидравлическая крупность наносов W=0,0015 м/сек.
Скачать решение задачи 5.33 (Решебник 4) (цена 60р)
Задача 5-34. Можно ли запроектировать незаиливаемый канал для пропуска Q=2,5 м3/сек при р=2 кг/м3, W=0,0008 м/сек, если n=1, п=0,0275, а i = 0,00036.
Скачать решение задачи 5.34 (Решебник 4) (цена 60р)
Задача 5-35. Определить ширину трапецеидального канала по дну при следующих данных: Q = 5,2 м3/сек; h=1,2 м; m=1; n=0,025; i= 0,0006.
Скачать решение задачи 5.35 (Решебник 4) (цена 60р)
Задача 5-36. Определить глубину наполнения трапецеидального канала, пропускающего расход Q=3,0 м3/сек при m=1; i=0,001; b-2м; n=0,017.
Скачать решение задачи 5.36 (Решебник 4) (цена 60р)
Задача 5-37. Рассчитать трапецеидальный бетонированный канал гидравлически наивыгоднейшего профиля при Q = 44 м3/сек; n = 0,014; i = 0,002; m = 0,75. Определить также среднюю скорость движения воды.
Скачать решение задачи 5.37 (Решебник 4) (цена 60р)
Задача 5-38. Рассчитать трапецеидальный канал для пропуска расхода Q = 10 м3/с при m = 1,25; i = 0,0004; n = 0,0225. Отношение ширины канала по дну h к глубине наполнения А принять равный b/h = 4,1.
Скачать решение задачи 5.38 (Решебник 4) (цена 60р)
Задача 5-39. Определить размеры трапецеидального канала при пропуске расхода Q = 19,6 м3/с со скоростью v = 1,30 м/с, если m = 1; n = 0,025; i = 0,0007.
Скачать решение задачи 5.39 (Решебник 4) (цена 60р)
Задача 5-40. Определить значение параметра р для капала параболического сечения при Q = 12,9 м3/с; h = 2,1 м; n = 0,020; i = 0,0005.
Скачать решение задачи 5.40 (Решебник 4) (цена 60р)
Задача 5-41. Определить глубину наполнения канала параболического сечения при пропуске расхода Q = 11,2 м3/сек, если P = 2,9 м; n = 0,0225; i = 0,0003.
Скачать решение задачи 5.41 (Решебник 4) (цена 60р)
Задача 5-42. Рассчитать канал параболического сечения при Q=9,1 м3/сек, n=0,025, i=0,0006 так, чтобы v=0,9 м/сек.
Скачать решение задачи 5.42 (Решебник 4) (цена 60р)
Задача 5-43. Рассчитать лоток сегментного сечения для пропуска расхода Q=5 м3/сек при i=0,0009, n=0,014, если е=0,15 м (см. рис. 5-3).
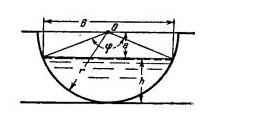
Скачать решение задачи 5.43 (Решебник 4) (цена 60р)
Задача 5-44. Определить глубину наполнения судоходного канала (рис. 5-11) полигонального сечения для пропуска расхода Q =80 м3/c, если i=0,0001; n=0,025.
Скачать решение задачи 5.44 (Решебник 4) (цена 60р)
Задача 5-63. Установить наибольший гидравлический радиус при проектировании трапецеидального канала с уклоном i=0,0004 в тяжелых суглинках на пропуск расхода Q=10 м3/сек.
Скачать решение задачи 5.63 (Решебник 4) (цена 60р)
Задача 5-64. Установить наименьший гидравлический радиус при проектировании канала с уклоном i=0,0002 и n = 0,0275, если средневзвешенная гидравлическая крупность наносов W=0,0018 м/сек при мутности потока р = 2 кг/м3.
Скачать решение задачи 5.64 (Решебник 4) (цена 60р)
Задача 5-65. Установить наибольший; гидравлический радиус при проектировании параболического канала с i=0,0009, Q = 15 м3/с, n = 0,020, vp=1,5м/с.
Скачать решение задачи 5.65 (Решебник 4) (цена 60р)
Задача 5-67. Запроектировать параболический канал для пропуска расхода Q=26 м3/сек при n=0,020; i=0,0004, если мутность потока р = 4,5 кг/м3, средневзвешенная гидравлическая крупность наносов W=0,0008 м/сек, а предельная скорость, не вызывающая размыва vраэн = 1,2 м/сек.
Скачать решение задачи 5.67 (Решебник 4) (цена 60р)
Задача 5-68. Запроектировать канал для пропуска расхода Q = 58 м3/ сек при n=0,025, i=0,0006, если мутность воды характеризуется р=3 кг/м3; средневзвешенная гидравлическая крупность наносов W=0,0035 м/сек; предельная скорость, не вызывающая размыва, vразм = 1,4 м/сек; заложение откосов канала m = 1,25.
Скачать решение задачи 5.68 (Решебник 4) (цена 60р)
Задача 5-69. Запроектировать трапецеидальный канал из условия его неразмываемости и незаиляемости при пропуске по нему следующих расходов: Qмакс=36 м3/сек; Qнорм = 25 м3/сек и Qмин = 16 м3/сек. Грунты - плотные глины. Канал в средних условиях содержания и ремонта. Мутность потока р-1,0 кг/м3. Средневзвешенная крупность наносов W=0,0035 м/сек. Уклон дна i = 0,0008.
Скачать решение задачи 5.69 (Решебник 4) (цена 60р)
Задача 5-70. Определить максимальное и минимальное значение уклона дна трапецеидального канала с учетом допускаемых скоростей, если Q = 1,5 м3/сек, m = 1,0; n = 0,0225; b = 2,32; р = 0,7 кг/м3; W = 0,00278 м/с; vразм = 0,7 м/с.
Скачать решение задачи 5.70 (Решебник 4) (цена 60р)
Задача 6-15. Трапецеидальный канал с b=10 м; m=1,25; n=0,020; i=0,001 пропускает расход Q=22 м3/сек. На канале поставлен щит, вызвавший подъем горизонта воды на 0,53 ж по сравнению с нормальным его положением. Определить тип кривой свободной поверхности и рассчитать эту кривую. Расчет выполнить по способам Б. А. Бахметева, Н. И. Павловского, И. И. Агроскина и по способу суммирования.
Скачать решение задачи 6.15 (Решебник 4) (цена 60р)
Задача 6-17: В бетонированном трапецеидальном канале (n=0,017) благодаря устроенному перепаду образуется кривая спада. Произвести расчет кривой свободной поверхности в канале, если Q=15 м3/сек; b=5 м; m=1,5; i=0,002. Глубина перед перепадом
Скачать решение задачи 6.17 (Решебник 4) (цена 60р)
Задача 6-18. Рассчитать кривую свободной поверхности на водоскате быстротока прямоугольного сечения при следующих данных: (Q=18,7 м3/сек, b=6,2 м, n=0,014, i=0,08. Длина водоската 100 м.
Скачать решение задачи 6.18 (Решебник 4) (цена 60р)
Задача 6-20. Рассчитать кривую свободной поверхности в круговом (сегментном) лотке, оканчивающемся перепадом. Данные для расчета: Q=0,5 м3/сек; d=1,3 м; i = 0,0009; n=0,014.
Скачать решение задачи 6.20 (Решебник 4) (цена 60р)
Задача 6-40. Построить кривую свободной поверхности на водоскате быстротока прямоугольного сечения. Водоскат в плане имеет переменную ширину от bгр1 = 10 м до bГР2=2 м. Длина водоската 60 м. Q=10 м3/сек, n=0,017, i = 0,008.
Скачать решение задачи 6.40 (Решебник 4) (цена 60р)
Задача 6-41. Рассчитать переходный участок с горизонтальным дном для пропуска расхода Q=8 м3/сек с постоянной глубиной h=1,2 м при m = 0, n=0,030. Ширила в начале bГР1 = 0,95 м; ширина в конце bГР2=2,8 м.
Скачать решение задачи 6.41 (Решебник 4) (цена 60р)
Задача 7-1. Прыжок возникает в трапецеидальном русле при Q=16 м3/сек, b= 1 м, m=1,5. Определить сопряженную глубину h", если h' = 0,50 м.
Скачать решение задачи 7.1 (Решебник 4) (цена 60р)
Задача 7-7. В параболическом русле возникает прыжок со второй сопряженной глубиной h"=2,2 м. Найти первую сопряженную глубину h' и длину прыжка lа, если Q = 6,2 м3/с, а р=2,6 м.
Скачать решение задачи 7.7 (Решебник 4) (цена 60р)
Задача 7-17. Определить вторую сопряженную глубину прыжка в .прямоугольном расширяющемся русле при следующих, данных: b1=3 м, h'=0,4 м; Q=7,25 м3/сек. Угол расширения русла в плане 0 = 5°.
Скачать решение задачи 7.17 (Решебник 4) (цена 60р)
Задача 7-18. Установить характер сопряжения потоков в прямоугольном лотке шириной b=10 м при изменении уклона от i1=0,05 до i2=0,00078, если Q=20 м3/сек, а нормальные глубины равны соответственно h01= 0,29 м; h02 = 1,09 м.
Скачать решение задачи 7.18 (Решебник 4) (цена 60р)
Задача 8-7. Определить ширину b прямоугольного водослива с острым ребром при следующих расчетных данных: расход воды Q = 520 л/сек, Р=0,4 м, H=0,35 м. Ширина подводящего (прямоугольного) канала В = 2,4 м.
Скачать решение задачи 8.7 (Решебник 4) (цена 60р)
Задача 8-10. Определить расход Q через щелевой водослив, имеющий при трапецеидальных водосливных отверстия (рис. 8-16), с шириной по низу b = 0,30 м, углами наклона боковых ребер а = 30°. Напор перед водосливом H=1,25 м. Коэффициент расхода принять m = 0,48.
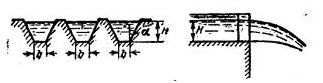
Скачать решение задачи 8.18 (Решебник 4) (цена 60р)
Задача 8-40. Водосливная плотина поддерживает в верхнем бьефе уровень НПУ 36,5 м. При пропуске паводочного расхода Qмакс=440 м3/сек подъем ВБ допускается до отметки ПУВВ 38,0 м. Определить ширину b, водосливной части плотины и необходимое количество щитовых отверстий (по типу рис. 8-23), если заданы размеры затворов 2,5X6,0 м. Ширина основного русла реки в створе плотины В = 70 м. Отметка дна 29,8 м. При Омане отметка УНБ 33,6 м.
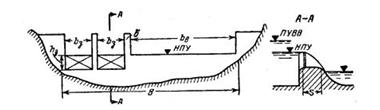
Скачать решение задачи 8.40 (Решебник 4) (цена 60р)
Задача 8-43. Определить высоту Р водослива из условия заданного подпора воды. Плотина в паводок пропускает расход Qнач=380 м3/сек при отметке УВБ 42,0 м. Максимальный расчетный расход Qмакс=470 м3/сек, при пропуске которого уровень воды в ВБ не должен превышать отметку 43,0 м. Оголовок плотины по типу I при Hпр=Нпав. Ширина водослива &=35,0 м. Ширина реки В=50 м. Отметка дна 32,0 л. В НБ уровень паводка 37,5 м, максимальный уровень 39,1 м.
Скачать решение задачи 8.43 (Решебник 4) (цена 60р)
Задача 8-51. Определить расход Q через водослив с широким порогом (рис. 8-27), если Н=0,85 м, Р = 0,50 м, h0 = 1,12 м, ширина водослива равна ширине подводящего канала b = 1,28 м.

Скачать решение задачи 8.51 (Решебник 4) (цена 60р)
Задача 8-57. Водослив шириной b=5,0 м имеет высоту порога P=1,0 м. Глубина перед водосливом h1=2,65м=const. Входная часть прямоугольная в плане и профиле (рис. 8-27). Бокового сжатия нет. Определить расход Q через водослив в двух случаях: при глубине за водосливом hв=2,0 м и при глубине hб=2,55 м.
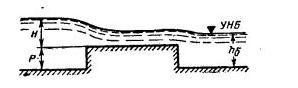
Скачать решение задачи 8.57 (Решебник 4) (цена 60р)
Задача 8-59. Определить .ширину b между опорами моста над трапецеидальным каналом при следующих условиях: расход воды в канале Q = 14,8 м3/сек, hб= 1,90 м, m=1,5, ширина канала по дну bк=7,0 м, опоры моста имеют прямоугольную форму в плане. Подпор воды перед мостом не должен превышать z=0,20 м (рис. 8-28).

Скачать решение задачи 8.59 (Решебник 4) (цена 60р)
Задача- 8-63. Регулятор в голове магистрального канала (рис. 8-29) имеет два пролета шириной b = 5,0 м каждый. Порог регулятора устроен заподлицо с дном канала и водохранилища на отметке 0. Канал имеет ширину по дну bm= 13,0 м и полуторные откосы. Определить расход Q через регулятор при отметке уровня воды в водохранилище 3,0 жив канале 2,7 м.
Скачать решение задачи 8.63 (Решебник 4) (цена 60р)
Задача 9-1. Определить глубину в сжатом сечении струи, переливающейся через водослив практического профиля (m=0,49, ф =0,95). Высота водослива Р=7 м (рис. 9-1), расход на 1 л ширины пролета q=8 м3/сек-м. Выяснить форму сопряжения потока в нижнем бьефе, если бытовая глубина hб=3 м.
Скачать решение задачи 9.1 (Решебник 4) (цена 60р)
Задача 9-7. Определить расход Q, вытекающий из-под плоского затвора, если высота открытия a=0,75 м, а напор H=3 м. Ширина отверстия, перекрываемого затвором, b=3,80 м равна ширине канала. Отверстие без порога. Глубина в нижнем бьефе hб=1,50 м.
Скачать решение задачи 9.7 (Решебник 4) (цена 60р)
Задача 9-9. На канале устроен перепад высотой Р=1,5 м (рис. 9-14). Нормальная глубина в канале h0=hб = 1,2 м. На какую высоту нужно поднять плоский затвор, чтобы пропустить расход Q=5 м3/сек, не нарушив равномерное движение в расположенном выше канале. Входная часть прямоугольного сечения шириной b =3,6 м. Ширина отверстия, перекрываемого затвором, также равна 3,6 м.
Скачать решение задачи 9.9 (Решебник 4) (цена 60р)
Задача 9-12. Определить расход, вытекающий из-под плоского затвора, поднятого на высоту а=0,6 м, если H=2,2 м, ширина отверстия b=3 м. Бытовая глубина в нижнем бьефе hб=1,8 м. Отверстие прямоугольное без порога (ф=0,97).
Скачать решение задачи 9.12 (Решебник 4) (цена 60р)
Задача 9-15. На гребне водослива практического профиля установлены плоские затворы для регулирования горизонта в верхнем бьефе (рис. 9-5). Определить, на какую высоту а нужно поднять затвор, чтобы пропустить через одно отверстие расход Q=30м3/сек, если H=3,6 л, b=5 м. Скоростным напором при подходе к плотине пренебречь.
Скачать решение задачи 9.15 (Решебник 4) (цена 60р)
Задача 9-17. Рассчитать глубину водобойного колодца прямоугольного сечения для сооружения, показанного на рис. 9-12, пренебрегая перепадом при выходе потока из водобойного колодца. Расход Q=12 м3/сек, ширина b=4 м, Hо=1,8 м, высота порога Р=2 м. Бытовая глубина в канале hб = 1,6 м.
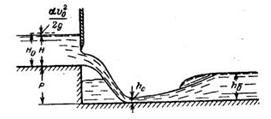
Скачать решение задачи 9.17 (Решебник 4) (цена 60р)
Задача 9-18. Рассчитать глубину d и длину водобойного колодца прямоугольного сечения при падении струи с водослива с широким порогом (рис. 9-11), если H0=2,4 м, Q=29,4 м3/сек. Ширина колодца равна ширине входной части b = 6,2 м. Высота падения Р=2,5 м. Коэффициент скорости, учитывающий 'боковое сжатие потока, поступающего из канала во входную часть, и потери по длине водослива, ф=0,85. Бытовая глубина hб=2 м. Перепадом z при выходе потока из колодца пренебречь.
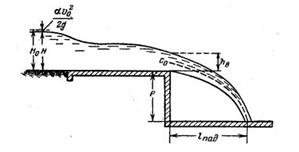
Скачать решение задачи 9.18 (Решебник 4) (цена 60р)
Задача 9-21. Рассчитать высоту водобойной стенки в условиях плоской задачи и проверить характер сопряжения потока за стенкой при следующих данных: высота водосливной плотины практического профиля Р=6 м, Н0=2м, q=6м3'/с-м. Бытовая глубина hб=3 м. Определить расстояние от сжатого сечения до водобойной стенки. Коэффициент скорости для плотины ф1=0,95, для водобойной стенки ф2=0,90.
Скачать решение задачи 9.21 (Решебник 4) (цена 60р)
Задача 9-23. Рассчитать высоту водобойной стенки на ступени перепада, если высота предыдущей ступени вместе со стенкой, т. е. высота падения, составляет H =3,4 м (рис. 9-17), Q = 15 м3/сек, ширина перепада прямоугольного сечения b=4,4 м, m=0,42, ф=0,9. Водобойная стенка работает как неподтопленный водослив. Определить длину ступени до переднего ребра водобойной стенки lст.
Скачать решение задачи 9.23 (Решебник 4) (цена 60р)
Задача 9-24. Рассчитать комбинированный водобойный колодец у плотины (рис. 9-9) при следующих данных: q = 8 м3/сек-м, высота плотины Р=7 м, Hо=3 м, глубина в нижнем бьефе hб=3 м, коэффициент скорости для плотины ф1=0,95; для водобойной стенки ф2=0)90. Расчет высоты водобойной стенки выполнить так, чтобы сопряжение переливающейся через стенку струи с потоком нижнего бьефа происходило в форме прыжка о сжатом сечении.
Скачать решение задачи 9.24 (Решебник 4) (цена 60р)
Задача 9-25. Рассчитать комбинированный водобойный колодец для условий, приведенных в предыдущей задаче, с той разницей, чтобы за водобойной стенкой сопряжение струи с потоком нижнего бьефа происходило в форме надвинутого прыжка и относительное подтопление было бы 0,6.
Скачать решение задачи 9.25 (Решебник 4) (цена 60р)
4.1 Решение задач маш гидравлика 4
Задача 1.1 Чему будет равна высота ртутного столба h2 (рис. 1.7), если манометрическое давление нефти в баллоне А РА = 0,5 кгс/см2, а высота столба нефти (рн = 7848 Н/м3 = 800 кг/м3) h1 = 55 см.
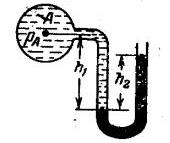
Скачать решение задачи 1.1 (Решебник 2) (цена 60р)
Задача 1.5 Определить плотность материала бруса, имеющего следующие размеры: ширина b = 300 см, высота h = 20 см и длина l = 100 см, если его осадка у = 16 см.
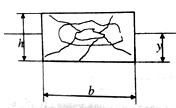
Скачать решение задачи 1.5 (Решебник 2) (цена 60р)
Задача 1.6 Определить вес поплавка диаметром D = 20 см, который при слое бензина H >80 см обеспечивал бы автоматическое открытие клапана диаметром d = 4 см (рис. 1.12). Длина тяги h = 74 см. Вес клапана и тяги принять 1,7Н = 0,173 кг. Относительная плотность бензина 0,75.
Скачать решение задачи 1.6 (Решебник 2) (цена 60р)
Задача 1.10 Прямоугольный клапан размерами а x b = 0,5 х 0,6 м закрывает отверстие в дне резервуара. Масса клапана G = 12 кг. Глубина воды в резервуаре h = 2 м. Клапан может вращаться шарнирно у оси А (рис. 1.14). Определить на каком расстоянии Х от шарнира нужно прикрепить трос, чтобы при подъеме получить наименьшее усилие Т? 2) величину этого усилия; 3) чему равнялось бы усилие Т, если бы трос был прикреплен в середине клапана (х = 0,25 м)? Трение не учитывать.
Скачать решение задачи 1.10 (Решебник 2) (цена 60р)
Задача 1.12 Деревянный брус размером 5,0 х 0,30 м и высотой 0,3 м спущен в воду. На какую глубину он погрузиться, если относительный вес бруса 0,7? Определить сколько человек могут встать на брус, чтобы верхняя поверхность бруса оказалась западлицо со свободной поверхностью воды, считая, что каждый человек в среднем имеет массу 67,5 кг.
Скачать решение задачи 1.12 (Решебник 2) (цена 60р)
Задача 1.16 Определить среднюю скорость движения воды в трубе при расходе 360 м3/ч и диаметре трубопровода 0,3м
Скачать решение задачи 1.16 (Решебник 2) (цена 60р)
Задача 1.18 Найти среднюю скорость жидкости v2 во втором сечении трубопровода площадью 0,4 м2, если в первом сечении площадью 0,1 м2, скорость v1 = 4м/с.
Скачать решение задачи 1.18 (Решебник 2) (цена 60р)
Задача 1.20 Найти среднюю скорость жидкости v2 во втором сечении трубопровода площадью 0,01 м2, если в первом сечении площадью 0,005 м2, скорость v1 = 4м/с.
Скачать решение задачи 1.20 (Решебник 2) (цена 60р)
Задача 1.21 Сосуд, имеющий наклонную боковую стенку, заполнен водой. В наклонной стенке сосуда имеется отверстие, перекрытое квадратной крышкой (поворачиваемый относительно шарнира) со стороной a=0,5 м. Крышка установлена на высоте H=2 м от поверхности сосуда. Угол наклона боковой стенки а=45 градусов. Найти силу R, необходимую для открытия крышки.
Скачать решение задачи 1.21 (Решебник 2) (цена 60р)
Задача 1.22 Определить показание вакуумметра hв (мм.рт.ст), установленного на маслобаке (рис. 1.19), если относительная плотность масла ,бм = 0,85, Н = 1,2 м, h = 150мм. Плотность ртути 13600 кг/м3.
Скачать решение задачи 1.22 (Решебник 2) (цена 60р)
Задача 1.27 Определить абсолютное давление воздуха в сосуде (рис. 1.23), если показание ртутного прибора h = 368 мм, высота Н = 1 м. Плотность ртути р=13600 кг/м3. Атмосферное давление 736 мм.рт.ст
Скачать решение задачи 1.27 (Решебник 2) (цена 60р)
Задача 1.28 Определить избыточное давление Р0 воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты Н должен быть пьезометр для измерения того же давления Ро:. Плотность ртути ppm = 13600 кг/м3
Скачать решение задачи 1.28 (Решебник 2) (цена 60р)
Задача 2.3 Вода течет по трубопроводу диаметром d = 150 мм со скоростью 6 м/с. Внизу вода растекается во все стороны по радиусу между двумя круглыми параллельными пластинками диаметром D = 800 мм, расположенными на расстоянии а = 30 мм одна от другой (рис. 2.4). Пренебрегая потерями напора, определить давление в точках В, отстоящих на расстоянии D/4 = 200мм от центра А, считая, что вода вытекает в атмосферу
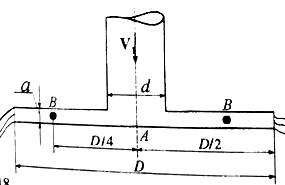
Скачать решение задачи 2.3 (Решебник 2) (цена 100р)
Задача 2.7 Для условий предыдущей задачи определить потери напора и разность давлений, вызванную внезапным расширением, если диаметр меньшей трубы равен 50мм, а большей равен по-прежнему 100мм. Расход воды 5000 см?/с
Скачать решение задачи 2.7 (Решебник 2) (цена 60р)
Задача 2.8 1. Определить расход воды, протекающий по горизонтальному трубопроводу диаметром 75 мм, если напор в резервуаре над центром выходного сечения трубы 1,5 м, длина трубопровода 5 м. Истечение происходит в атмосферу. Скоростным напором в резервуаре можно пренебречь. 2. Какой расход пропустит при том же напоре трубопровод, если его длину увеличить на 35 м? 3. Какой потребовался бы напор H в последнем случае, чтобы расход остался таким же как в первом случае
Скачать решение задачи 2.8 (Решебник 2) (цена 100р)
Задача 2.10 По трубе диаметром d1 = 40мм подается вода со скоростью v1 = 4,96 см/с при температуре t = 12°С. Труба постепенно сужается до диаметра d2 = 20 мм. Определить расход воды и режим движения в широкой и узкой частях трубы
Скачать решение задачи 2.10 (Решебник 2) (цена 60р)
Задача 2.11 Определить для предыдущей задачи, какой расход воды нужно подавать по трубам, чтобы в широкой части диаметром d = 40мм установился турбулентный режим. Чему будет равно число Рейнольдса в суженной части трубы при этом расходе?. Температура воды t = 12°С.
Скачать решение задачи 2.11 (Решебник 2) (цена 60р)
Задача 2.12 Треугольный лоток с коэффициентом заложения откоса m=1 используется в лаборатории для сброса воды. Определить режим движения (Rer) при пропуске расхода Q=3,2 л/с, если глубина воды в лотке h=8 см, v=0,0131 см?/с
Скачать решение задачи 2.12 (Решебник 2) (цена 60р)
Задача 2.16 Для условия предыдущей задачи определить потери напора, если расход в трубопроводе будет не 100 л/с, а Q = 40 л/с, l = 500м, d = 250 мм, = 1,35мм. Температура воды t = 10°C
Скачать решение задачи 2.16 (Решебник 2) (цена 60р)
Задача 2.27 Бензин сливается из цистерны (рис. 2.16) по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления Cкр = 3. Определить расход бензина при Н1 = l,5 м и Н2 = 1,3 м, если в верхней части цистерны имеет место вакуум hвак = 73,5 мм рт. ст. Потерями на трение в трубе пренебречь. Плотность бензина p = 750 кг/м3.
Скачать решение задачи 2.27 (Решебник 2) (цена 100р)
Задача 2.31 Вода перетекает по трубе из бака А (рис. 2.20) в резервуар Б через вентиль с коэффициентом сопротивления 3. Диаметры d1 = 40мм, d2 = 60мм. Считая режим течения турбулентным и, пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты Н1 = 1м, Н2 = 2м; избыточное давление в напорном баке Р0 = 0,15 МПа
Скачать решение задачи 2.31 (Решебник 2) (цена 100р)
Задача 3.2 Определить потери давления на участке трубопровода, представленного на рис. 3.2, если известна скорость движения потока жидкости V = 3 м/с и плотность жидкости ? = 1000 кг/ м3 . Коэффициенты местных потерь С1 = 6; С2 = 1,2; С3 = 1,7; С4 = 0,8. С5 = 6. Потерями на трение по длине пренебречь.
Скачать решение задачи 3.2 (Решебник 2) (цена 60р)
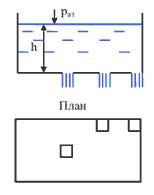
Задача 3.3 Квадратное отверстие в стенке резервуара примыкает одной стороной а = 3,6см ко дну (рис. 3.6). Определить при какой глубине h воды в резервуаре расход через отверстие будет Q = 4,18 л/с
Скачать решение задачи 3.3 (Решебник 2) (цена 80р)
Задача 3.4 В дне бака расположены три одиннаковых квадратных отверстия со стороной а = 3,5 см. Одно отверстие в центре дна, другое – одной стороной примыкает к боковой стенке, треть расположено в углу дна (рис. 3.7). Глубина воды в баке h = 85см. Определить 1. Суммарный расход Q1 из отверстий, если давление на поверхности воды атмосферное Р0 = 1 атм; 2. Суммарный расход Q2 из отверстий, если давление на поверхности воды атмосферное Р0 = 1,8 атм;
Скачать решение задачи 3.4 (Решебник 2) (цена 100р)
Задача 3.7 Определить диаметр d горизонтальной цилиндрической насадки, расположенной в стенке бака на расстоянии e = 1,0 м от дна, чтобы за время t=10 мин через насадку пропустить половину начального объема воды в баке. Диаметр бака D=1,6 м. Глубина воды в баке до открытия насадки h=3,18 м.
Скачать решение задачи 3.7 (Решебник 2) (цена 60р)
Задача 3.9. Определить скорость перемещения поршня вниз (рис. 3.12), если к его штоку приложена сила F=10 кН. Поршень диаметром D = 50 мм имеет пять отверстий диаметром d0 = 2 мм каждое. Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода 0,82; р = 900 кг/м3.
Скачать решение задачи 3.9 (Решебник 2) (цена 60р)
Задача 4.2. В вертикальной стенке, разделяющей открытый резервуар на две части, расположено отверстие диаметром d1 = 50 мм. В наружной стенке имеется другое отверстие диаметром d2. Центры обоих отверстий расположены на высоте h=l,0 м от дна. Глубина воды в левой части резервуара 2,5 м; расход через отверстия Q = 3,l л/с. Определить глубину h2 воды в правой части резервуара и диаметр d2 отверстия в наружной стенке.
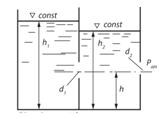
Скачать решение задачи 4.2 (Решебник 2) (цена 60р)
Задача 4.3 Определить скорость истечения жидкости через насадок диаметром d = 10 мм, если высота жидкости h = 1 м и плотность ρ = 900 кг/ м3. Избыточное давление в баке P = 0,03 МПа.
Скачать решение задачи 4.3 (Решебник 2) (цена 60р)
Задача 4.4 Жидкость с плотностью р = 900 кг/м3 и вязкостью v = 0,001 Ст нагнетается по горизонтальному трубопроводу длиной l = 4м и диаметром d = 25мм. Определить давление в начальном сечении, если в конечном сечении трубопровода давление атмосферное, расход жидкости Q = 6л/с, шероховатость стенок трубопровода 0,06.
Скачать решение задачи 4.4 (Решебник 2) (цена 60р)
Задача 4.9 Вода по трубе 1 подается в открытый бак и вытекает по трубе 2. Во избежание переливания воды через край бака устроена вертикальная сливная труба 3 диаметром d = 50 мм. Определить необходимую длину L трубы 3 из условия, чтобы при Q1 = 10 л/с и перекрытой трубе 2 (Q2 = 0) вода не переливалась через край бака. Режим течения считать турбулентным. Принять следующие значения коэффициентов сопротивления: на входе в трубу C1=0,5; в колене C2 = 0,5; на трение по длине трубы т = 0,03; а = 0.
Скачать решение задачи 4.9 (Решебник 2) (цена 60р)
Задача 5.2 Керосин перекачивается по горизонтальной трубе длиной l = 50 м и диаметром d = 0,03 м в количестве Q = 0,0098 м3/с. Определить потребное давление и необходимую мощность, если свойства керосина: v = 0,025*10-4 м2/с; p = 800 кг/м3. Местными гидравлическими сопротивлениями пренебрегаем.
Скачать решение задачи 5.2 (Решебник 2) (цена 60р)
Решение задач часть 1 Статика жидкости
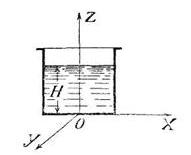
Задача 1. Определить свободную поверхность и закон распределения давления в случае однородной тяелой покоящейся жидкости (рис. 16).
Скачать решение задачи 1 (Решебник 4) (цена 60р)
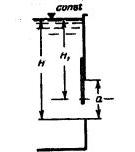
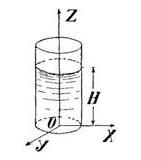
Задача 2. Сосуд, наполненный однородной тяжелой жидкостью, движется по вертикали равноускоренно. Определить свободную поверхность и давление на дне сосуда (рис. 17).
Скачать решение задачи 2 (Решебник 4) (цена 60р)
Задача 3. Паровой движется по горизонтальному и прямолинейному пути с постоянным ускорением w. Определить распределение давлений и уравнение свободной поверхности в тендере паровоза (рис. 18).
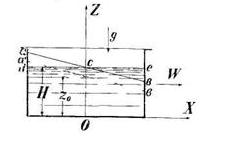
Скачать решение задачи 3 (Решебник 4) (цена 60р)
Задача 4. По наклонной плоскости, составляющей с горизонтом угол У, движется под влиянием силы тяжести без сопротивления сосуд, наполненный водою. Определить уравнение свободой поверхности и закон распределения давлений (рис. 19)
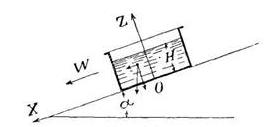
Скачать решение задачи 4 (Решебник 4) (цена 60р)
Задача 5. Определить свободную поверхность и закон распределения давлений в случае однородной тяжелой газообразной покоящейся жидкости. Поверхности равных давлений суть горизонтальные плоскости, которые определяются совершенно так же, как и в задаче 1.
Скачать решение задачи 5 (Решебник 4) (цена 60р)
Задача 6 Открытый цилиндрический сосуд, радиуса R, наполненный до высоты Н тяжелой жидкостью, приведен в равномерное вращательное движение вокруг вертикальной оси 2, совпадающей с осью сосуда. Угловая скорость вращения равна w. Определить свободную поверхность и распределение давлений (рис. 20).
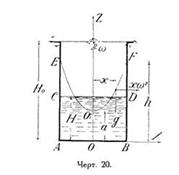
Скачать решение задачи 6 (Решебник 4) (цена 60р)
Задача 7. Река шириною в 1 клм. течет по закруглению (рис. 21) со скоростью V = 6км/ч Предполагая, что скорости всех частиц воды в одном и том же сечении равны геометрически и пренебрегая вращением земли, определить превышение внешнего берега над внутренним.
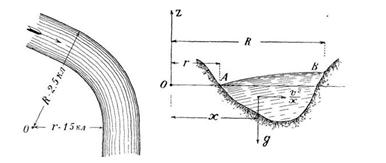
Скачать решение задачи 7 (Решебник 4) (цена 60р)
Задача 8. Верхне-наливное гидравлическое колесо равномерно вращается с углового скоростью w вокруг горизонтальной оси х. Определить свободную поверхность жидкости в ковшах колеса (рис. 22).
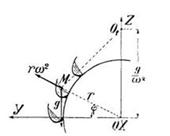
Скачать решение задачи 8 (Решебник 4) (цена 60р)
Задача 9. Невесомая однородная жидкость притягивается к неподвижному центру по закону, выражающемуся некоторой функцией расстояния. Определить поверхности равных давлений (рис. 23),
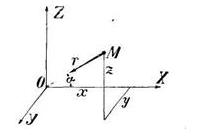
Скачать решение задачи 9 (Решебник 4) (цена 60р)
Задача 10. Невесомая однородная жидкость, вращающаяся с постоянной угловой скоростью (о вокруг вертикальной оси z-ов, притягивается точкою О, лежащею на оси вращении, силою пропорциональною расстоянию К. Определить свободную поверхность жидкости и распределение давлений (рис. 24).
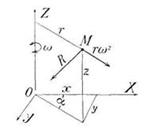
Скачать решение задачи 10 (Решебник 4) (цена 60р)
Задача 11. Река шириною 2L = 1 км. течет с юга на север со скоростью v=5км/ч. Определить, учитывая вращение земли вокруг ее оси, у какого берега вода выше и насколько в сечении, находящемся на 60 северной широты (рис. 25).
Скачать решение задачи 11 (Решебник 4) (цена 60р)
Задача 12. Определить давление на единицу площади дна сосуда, на глубине Н = 1,5 м под поверхностью, считая, что на поверхности давление равно 2 атм. в двух предположениях: 1) сосуд наполнен водой (у = 1) и 2) сосуд наполнен спиртом (у = 0,80).
Скачать решение задачи 12 (Решебник 4) (цена 60р)
Задача 13. Определить высоту воды в сосуде, площадь дна которого Р = 0,12 м2, а давление на дно Р = 24 кг.
Скачать решение задачи 13 (Решебник 4) (цена 60р)
Задача 14. В горизонтальном дне сосуда сделано отверстие, закрываемое задвижкою, площадь которой F= 2,5 см-5; высота воды в сосуде Н = 1,5 м. Какую силу нужно приложить к задвижке, чтобы открыть отверстие, если коэффициент трения f= 0,5.
Скачать решение задачи 14 (Решебник 4) (цена 60р)
Задача 15. Два сообщающихся сосуда заполнены жидкостями, удельные веса которых y1 и y2. Давления на свободных поверхностях одинаковы. Разность уровней составляет h. Определить высоты h1 и h2 уровней над плоскостью раздела (рис. 26).
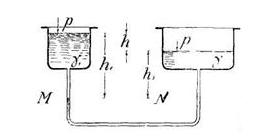
Скачать решение задачи 15 (Решебник 4) (цена 60р)
Задача 16. Два вертикальных цилиндра, имеющих диаметры d= 20 см. и D =40 см, наполнены водой и сообщены между собой трубкой. В цилиндры заключены поршни, из которых меньший стоит на h=30 см. выше, чем больший и несет нагрузку Р=80 кг. Какой груз надо положить на больший поршень, чтобы они находились в равновесии (трением пренебречь) (рис. 27).
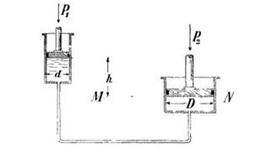
Скачать решение задачи 16 (Решебник 4) (цена 60р)
Задача 17. При атмосферном давлении h1= 765 мм. в цилиндр был вставлен свободно поршень и при атмосферном давлении h2= 750 мм. цилиндр был опущен в море; при этом начальное расстояние l1=20 см. между дном цилиндра и поршнем уменьшилось до l2= 3 см. Считая удельный вес морской воды y= 1,02 и предполагая температуру постоянной, определить глубину погружения цилиндра.
Скачать решение задачи 17 (Решебник 4) (цена 60р)
Задача 18. Наклонный трубопровод, имеющий клапан К, соединяет два закрытых резервуара, наполненных водой. В первом наблюдается манометрическое давление в 2 атм., во втором - вакуум в 0,3 атм. Определить давление на единицу площади клапана. Размеры в метрах указаны на рисунке 28.
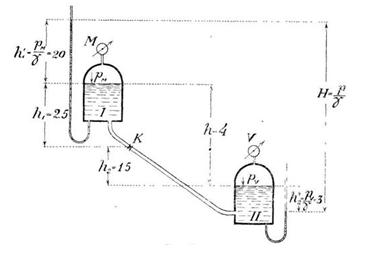
Скачать решение задачи 18 (Решебник 4) (цена 60р)
Задача 19. Определить сжимающее усилие гидравлического пресса, изображенного на рисунке 29, если: а = 2000, b = 100, D = 340, d= 15, (размеры в миллиметрах), Q = 20 кг. = (усилие одного рабочего).
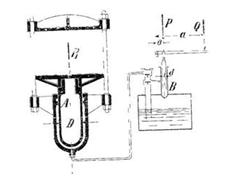
Скачать решение задачи 19 (Решебник 4) (цена 60р)
Задача 20. Определить по двухжидкостному манометру давление P, если известны удельные веса жидкостей y1 и y2 при чем y1<y2, расстояние между плоскостями раздела равно h и давление на открытой поверхности равно атмосферному (рис. 30).
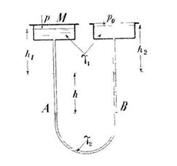
Скачать решение задачи 20 (Решебник 4) (цена 60р)
Задача 21. Определить двухжидкостным дифференциальным манометром разность давлений в А и В (см. рис. 14, на стр. 19) при данных удельных весах жидкостей y1 и y2 и расстоянии h между плоскостями раздела.
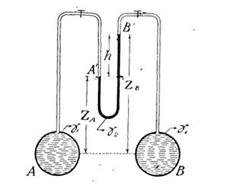
Скачать решение задачи 21 (Решебник 4) (цена 60р)
Задача 22. Плоский прямоугольный водоудержательный шит перегораживает канал шириною b= 3 м; глубина воды в канале Н = 2,5 м. Определить давление воды на щит и усилие, необходимое для подъема щита, если вес щита G = 1 т. и коэффициент трения f= 0,50 (рис. 31).
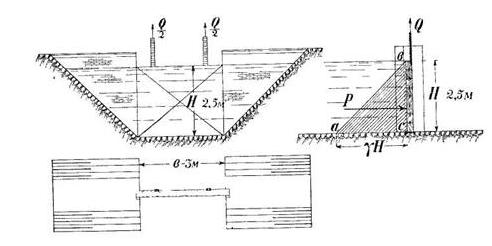
Скачать решение задачи 22 (Решебник 4) (цена 60р)
Задача 23. Шлюзовое окно закрыто дубовым щитом, высотою h= 2 м, шириною b= 1,8 м. и толщиною t = 6 см. Горизонт воды перед щитом на 1 м. выше его верхнего края. Определить подъемное усилие, если удельный вес дуба 1,2 и коэффициент трения f= 0,50, в двух случаях: 1)не принимая во внимание давления воды на верхнюю и нижнюю грани щита и 2) приняв таковые во внимание (рис. 32).
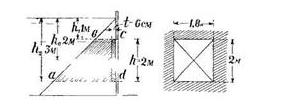
Скачать решение задачи 23 (Решебник 4) (цена 60р)
Задача 24. Плотина Таvernier. Система плоских щитов» поддерживаемых вращающимися стойками, перегораживает реку. Определить давление на щит и реакции шарнира А и порога В, если расстояние между стойками равно и= 2 м. Размеры указаны на рисунке 33.
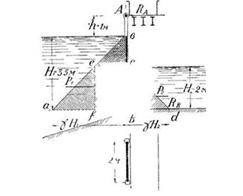
Скачать решение задачи 24 (Решебник 4) (цена 60р)
Cтраница 1 из 2


