Часть 11-2 Истечение под переменным напором
Задача (Куколевский И.И.) 11-24. Открытый цилиндрический сосуд (диаметром D = 1,5 м и высотой h = 1,6 м), внутри которого свободно помешается круглый, деревянный брус, плавает будучи погружен в воду на глубину h0 = 0,6 м. Диаметр бруса d = 0,8 м, его высота h1 = 0,8 м и относительная плотность δ = 0,75.
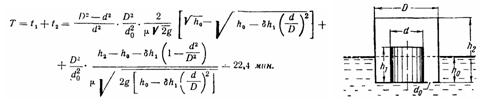
Определить время затопления сосуда с момента открытия донного отверстия диаметром h0 = 30 мм, коэффициент расхода которого равен μ = 0,62. Влиянием толщины стенок сосуда пренебрегать.
Указание. Затопление сосуда будет происходить при переменном напоре истечения через отверстие до момента всплытия- бруса, а затем - при постоянном напоре истечения.
Ответ
Задача (Куколевский И.И.) 11-25. Тонкостенный открытый призматический сосуд (шириной а = 2 м, длиной b = 5 м и высотой h = 1,8м), плавает в воде, погруженный на глубину h0 = 0,8 м. Сосуд снабжен двумя вертикальными тонкостенными переборками, расстояние между которыми с = 1,5 м. Рассмотреть процесс погружения сосуда после открытия в отсеке между переборками донного отверстия диаметром d0 = 40 мм (μ = 0,62), определив:
1) новую глубину погружения сосуда и время, в течение которого сосуд будет дополнительно погружаться;,
2) предельное расстояние между переборками Cmax, при котором сосуд с открытым донным отверстием может еще сохранять плавучесть.
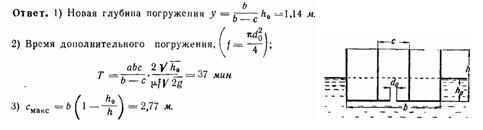
Скачать решение задачи 11-25 (Куколевский И.И.) (цена 100р)
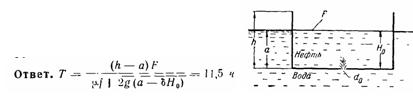
Задача (Куколевский И.И.) 11-26. Определить время затопления баржи, заполненной нефтью относительного удельного веса б=0,85 на высоту Н0 = 2 м после получения ею донной пробоины (диаметр отверстия d0 = 50 мм, μ = 0,61). Размеры баржи: высота h = 3 м, площадь F = 120 м2, ее начальное погружение а = 2 м.
Скачать решение задачи 11-26 (Куколевский И.И.) (цена 100р)
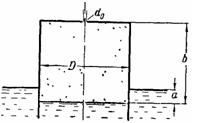
Задача (Куколевский И.И.) 11-27. Тонкостенный колокол начинает погружаться в воду из показанного на чертеже начального положения вследствие того, что в верхней его части образовалось отверстие, через которое сжатый воздух выходит наружу.
Определить без учета сжимаемости воздуха время полного погружения колокола при следующих данных: D = 1,5 м; а = 0,2 м; b = 2 м.
Диаметр отверстия d0 = 6 мм, его коэффициент расхода μ = 0,6. Плотность воздуха ρ = 1.2 кг/м3.
Ответ. Т =55 мин.
Задача (Куколевский И.И.) 11-28. Шестеренный насос откачивает бензин из двух баков одинаковой площади F = 8 м2 по трубам одинакового диаметра d = 50 мм и длины (до точки их смыкания) l=13 м.
Определить выработку из каждого бака за время Т =10 мин, если производительность насоса Q = 4 л/с, заполнение каждого бака равно h. = 1,5 м и начальная разность уровней бензина H = 1 м.
В трубах учитывать только потери на трение, принимая λ = 0,025. Сопротивлением дренажных трубок пренебрегать, считая, что давление в баках равно атмосферному. Указание. В момент времени t расходы Q1 и Q2 п трубах и разность z уровней и баках (см. рис. к решению задачи) связаны соотношением

Задача (Куколевский И.И.) 11-29. Пневмогидравлический аккумулятор диаметром D = 100 мм, заряженный избыточным давлением воздуха P0 = 5 МПа, подключен к гидроцилиндру диаметром D1 = 60 мм, по штоку которого приложена постоянная сила Р = 7100 Н Определить время полного хода поршня цилиндра S = 150 мм, предполагая режим движения в трубопроводе (l = 10 м, d = 6 мм) ламинарным и расширение воздуха в аккумуляторе изотермическим (a0 = 120 мм). Кинематический коэффициент вязкости жидкости v = 0,6 Ст, ее плотность ρ = 900 кг/м3. Атмосферное давление Pат = 0,1 МПа.
Определить время полного хода, если нагрузка увеличится до Р = 9000 Н.
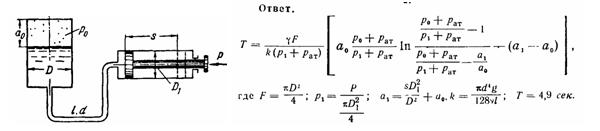
Задача (Куколевский И.И.) 11-30. Пневматический амортизатор шасси с диаметром цилиндра D = 120 мм в начальном положении заряжен воздухом под давлением P0 = 3,2 МПа, который занимает часть высоты цилиндра a0 = 150 мм.
Определить время и осадку цилиндра под действием постоянной нагрузки G = 50 кН, внезапно приложенной к амортизатору, если перетекание жидкости происходит через отверстие диаметром d = 3 мм (коэффициент расхода μ = 0,8). Удельный вес жидкости (спиртогляцериновая смесь) ρ = 1120 кг/м3. Указание. Дифференциальное уравнение процесса истечения

Задача (Куколевский И.И.) 11-31. Вода, заполняющая цилиндр аккумулятора, находится под давлением, создаваемым предварительно сжатой пружиной, жесткость которой равна С = 20 Н/см. Открытием крана К аккумулятор включается и жидкость благодаря действию пружины начинает вытекать через трубку, диаметр которой d = 10 мм и суммарный коэффициент сопротивления ξ = 4.
Определить время выработки (опорожнения) цилиндра аккумулятора, если его диаметр D = 110 мм и предварительное сжатие пружины в начальном положении поршня z0 = 60 мм. Высоты: а = 70 мм, b=30 мм.
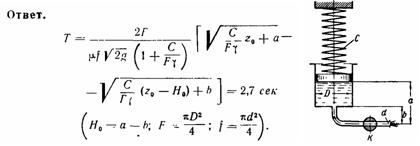
Задача (Куколевский И.И.) 11-32. Для аварийной остановки поездов в тупиках применяют двухцилиндровый гидравлический тормоз, в котором кинетическая энергия поезда поглощается работой гидравлического трения при перетекании воды через малое отверстие в поршне.
Найти уравнение у = f(х) профиля клина, перекрывающего дросселирующее прямоугольное отверстие шириной b = 52 мм, если торможение поезда массой m = 500 т, который подходит со скоростью v0 = 7,2 км/ч, должно происходить на пути s = 0,8 м и процесс торможения желают осуществить равнозамедленным. Диаметр цилиндра D = 300 мм. Давление в левой полости поддерживается равным P0 = 3 атм.
Коэффициент расхода дросселирующего отверстия принять постоянным и равным μ = 0,60.
Указание. При равнозамедленном движении поршня величина его замедления

Задача (Куколевский И.И.) 11-33. Определить время опорожнения сосуда диаметром D = 300 мм, заполненного жидкостью на высоту H = 600 мм, при равномерно ускоренном движении сосуда в двух случаях: 1) ускорение сосуда а = 2,5 м/с2 направлено вверх; 2) такое же по величине ускорение направлено вниз. Истечение происходит через отверстие d=25 мм (μ = 0,62).
Ответ.T = 72,7 сек; Т= 94,2 сек.
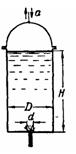
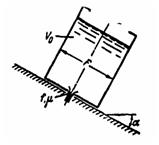
Задача (Куколевский И.И.) 11-34. Цилиндрический бак площадью F=0,5м2 свободно скользит без трения по наклонной плоскости под углом α = 30° к горизонту. В начальный момент бак содержит v0 = 0,6 м3 жидкости, которая вытекает при движении бака через донное отверстие площадью f = 5 см2 (коэффициент расхода (μ = 0,6). Какой объем выльется из бака за время t = 60 с?
Ответ. V = 80 л.
Задача (Куколевский И.И.) 11-35. Цилиндрический сосуд, диаметр которого D = 1 м и ширина B = 0,4 м, вращается вокруг горизонтальной оси с числом оборотов n = 1000 об/мин, В сосуде содержится V = 0,25 м3 жидкости. Определить время опорожнения сосуда через четыре отверстия диаметром d = 10 мм, расположенные на боковой поверхности сосуда. Коэффициент расхода отверстий принять μ = 0,65.
Ответ. Т = 52,5 сек.
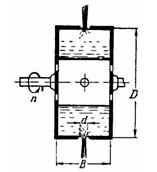
Задача (Куколевский И.И.) 11-36. Из сосуда диаметром D = 0,6 м, который вращается вокруг вертикальной оси с угловой скоростью w = 10 рад/с и закрыт сверху поршнем массой 282 кг, вытекает вода через четыре боковых отверстия (d = 10 мм; μ = 0,6). Определить, в течение какого времени будет продолжаться истечение, если в начальный момент отверстия расположены на глубине b = 0,3 м под поршнем. Трением поршня пренебречь.
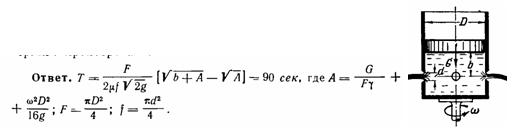
Скачать решение задачи 11-36 (Куколевский И.И.) (цена 100р)
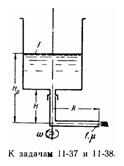
Задача (Куколевский И.И.) 11-37. Неподвижный призматический бак площадью F = 0,1 м2, заполненный жидкостью до уровня H0 = 1 м, опоражнивается через вращающуюся трубку сечением f = 1 см2, выходное отверстие которой удалено от оси вращения на расстояние R = 20 см и расположено ниже дна бака на H = 0,5 м.
Найти время Т опорожнения бака при неподвижной трубке и число ее оборотов, которое уменьшит время опорожнения в два раза. Коэффициент расхода трубки принимать независящим от числа ее оборотов и равным μ = 0,4.
Ответ. Т = 5,5 мин; n = 305 об /мин.
Задача (Куколевский И.И.) 11-38. Найти время опорожнения цилиндрического сосуда площадью F = 0,1 м2 через неподвижную трубку площадью поперечного сечения f = 1 см2 (коэффициент расхода трубки μ = 0,4), если сосуд, заполненный до начального уровня H0 = 1 м, приведен в равномерное вращение с угловой скоростью w = 10 рад/с. Выходное сечение трубки расположено на радиусе R = 20 см и на глубине H = 0,5 м ниже дна бака. Какое количество жидкости останется при этом в сосуде?
Ответ. 1) Т = 9 мин. 2) V0 = 10 л.
Задача (Куколевский И.И.) 11.39. Определить время затопления тонкостенного понтона призматической формы после получения им бортовой пробоины на глубине b = 0,5 м. Площадь пробоины f = 20 см2, ее коэффициент расхода μ = 0,6. Размеры понтона: высота h = 2 м и площадь дна F = 25 м2. Начальное погружение понтона в воду а = 1 м.
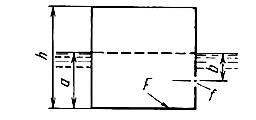
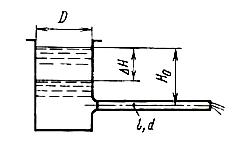
Задача (Куколевский И.И.) 11.40. Капиллярный вискозиметр имеет бачок диаметром D = 50 мм, из которого испытуемая жидкость вытекает в атмосферу по капилляру диаметром d = 1 мм и длиной l = 200 мм, расположенному горизонтально. Вязкость жидкости определяется по времени опускания уровня жидкости в бачке от начального положения Н0 = 50 мм на заданную величину ΔH = 25 мм.
Определить кинематическую вязкость жидкости, если время опускания уровня Т = 75 мин. Потерей напора при входе в капилляр, влиянием его начального участка и скоростным напором выхода пренебречь.
Ответ. v = 4 сСт.
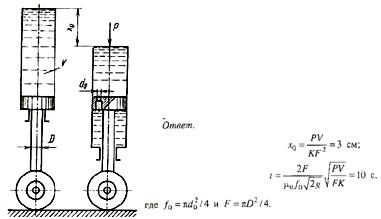
Задача (Куколевский И.И.) 11.41 К цилиндру гидравлического амортизатора (где в качестве пружины используется сжимаемая под нагрузкой жидкость) приложена сила Р = 400 кН. Считая стенки цилиндра абсолютно жесткими, определить величину опускания x0 цилиндра относительно поршня амортизатора (прямой ход) и время t обратного хода при внезапном прекращении действия силы Р. Дроссельное отверстие в поршне имеет диаметр d0 = 4 мм, его коэффициент расхода 0,6. Модуль упругости жидкости принять постоянным К = 12*108 Н/м2. Объем жидкости в ненагруженном цилиндре V = 5500 см3. Диаметр штока D= 100 мм. Силами инерции жидкости и цилиндра, а также силами трения пренебречь.
Задача (Куколевский И.И.) 11.42. Два одинаковых цилиндрических резервуара заполнены жидкостью до уровня h каждый и имеют донные отверстия площадью f1 и f2, коэффициенты расхода которых равны μ1, и μ2 соответственно. Отверстия открываются одновременно. Определить уровень у в нижнем резервуаре в тот момент, когда верхний резервуар будет полностью опорожнен.
Найти у в частном случае, когда μ1 = μ2, f1 = f2
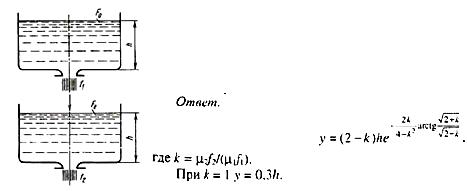
Скачать решение задачи 11-42 (Куколевский И.И.) (цена 100р)


