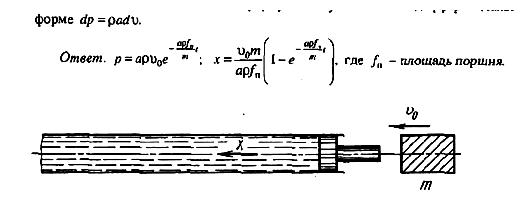
Часть 12 (Решение задач из сборника Куколевского)
Часть 12-1 Неустановившееся движение жидкости
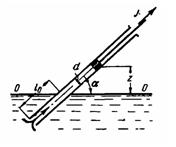
Задача (Куколевский И.И.) 12-1. В наклонной трубе (а = 45°), диаметр которой d = 60 мм, движется, увлекая за собой воду, поршень с постоянным ускорением j = 0,5 м/с2. Длина погруженной части трубы l0 = 2 м. Определить, на какой высоте zмакс над уровнем произойдет отрыв воды от поршня, если в начальный момент движения (при t=0 и z = 0) скорость поршня v = 0 и если наибольшая допустимая при заданной температуре воды вакууметрическая высота всасывания равна 8м.
Коэффициент сопротивления входа в трубу ξвх = 1; коэффициент сопротивления трения в трубе λ = 0,03.
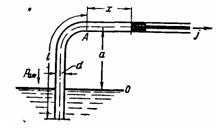
Задача (Куколевский И.И.) 12-2. Поршень, двигаясь в трубе вправо от сечения А, увлекает за собой жидкость с постоянным ускорением j = 1,5 м/с2. В начальном положении при x = 0 скорость V = 0.
Определить место отрыва xmax жидкости от поршня, если относительная плотность жидкости δ = 0,8, упругость ее насыщенных паров Pнп = 147 мм.рт.ст и атмосферное давление Рят = 735 мм рт.ст. Диаметр трубы d = 90 мм, ее длина до сечения А l = 5 м, высота а = 1 м. Коэффициент сопротивления трения λ = 0,03, коэффициент сопротивления входа в трубу ξвх = 1;
Ответ. xmax = 7,5м.
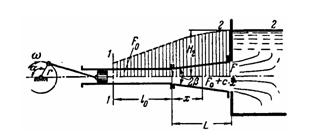
Задача (Куколевский И.И.) 12-3. Поршень, приводимый в движение кривошипно-шатунным механизмом, перемещает жидкость в трубе, заканчивающейся расходящимся коническим насадком, подключенным к резервуару, где уровень жидкости постоянен. Определить избыточное давление у поршня в тот момент, когда он находится в крайнем правом положении (а =180°), и построить пьезометрическую линию для этого момента времени.
Скачать решение задачи 12-3 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-4. Поршневой насос простого действия без воздушных колпаков перекачивает воду из нижнего бака в верхний, будучи расположен на высоте Н1 = 2 м над нижним уровнем. Уровень воды в верхнем баке выше оси насоса на H2 = 6,5 м. Длина всасывающей трубы l1 = 3 м, длина нагнетательной l2 = 7 м, их площади поперечного сечения f одинаковы и составляют половину площади F поршня Радиус кривошипа r = 0,1 м, чистота вращения n = 100 об/мин.
Определить абсолютное давление рх в рабочем цилиндре в начале хода всасывания и в конце хода нагнетания. Атмосферное давление принять равным 10 м вод. ст.
Ответ. рх = 15 и 12 кПа.
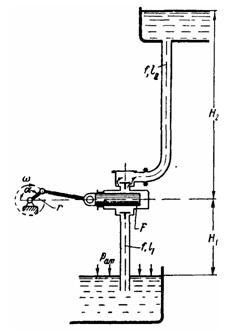
Скачать решение задачи 12-4 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-5. Однодействующий поршневой насос без воздушных колпаков присоединен к напорному трубопроводу длиной L = 35 м. В мертвой точке ускорение плунжера насоса j = 2,5 м/с2. Указать место разрыва сплошности движения воды в напорном трубопроводе, сечение которого равно 1/2 площади плунжера, считая, что разрыв наступает при снижении абсолютного давления до 26 кПа. Атмосферное давление считать равным 0,1 МПа.
Ответ. Разрыв сплошности движения воды будет иметь место в сечении 10м от конца трубы
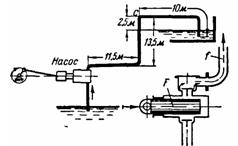
Скачать решение задачи 12-5 (Куколевский И.И.) (цена 100р)
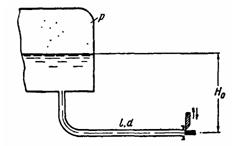
Задача (Куколевский И.И.) 12-6. Дозирующее устройство практически мгновенно открывает трубу (l = 50м, d = 60 мм) и затем также мгновенно вновь ее закрывает.
Определить избыточное давление Р, которое должно быть создано в резервуаре, чтобы за время Т = 2с, в течение которого труба остается открытой, вытекшее количество жидкости составляло W = 12 л. Уровень жидкости (р = 1000 кг/м3) в резервуаре Н0 = 1 м.
Коэффициент сопротивления трения в труде принять λ = 0,03, потерей входа пренебречь.
Ответ. P = 0,14 МПа.
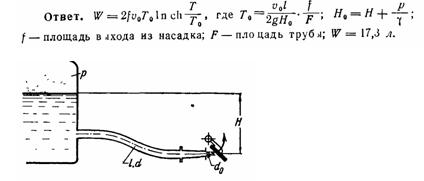
Задача (Куколевский И.И.) 12-7. Бензинопровод длиной l = 50 м и диаметра d = 60 мм, снабженный коническим насадком выходным диаметром d0 = 45 мм, открывается при помощи быстродействующего затвора.
Определить, какое количество бензина поступит из бака за время Т = 5 с с момента открытия затвора, если уровень бензина в баке H = 1,5 м, а избыточное давление в баке P = 0,05 МПа. Плотность бензина р = 750 кг/м3.
Коэффициент сопротивления трения принять λ = 0,03. Сопротивлением конического насадка пренебречь.
Задача (Куколевский И.И.) 12-8. Вертикальная труба диаметром d = 50 мм длиной l = 10 м с открытым верхним концом, полностью заполненная водой, начинает после открытия нижнего ее конца опорожняться в атмосферу.
Определить время полного опорожнения трубы, приняв в течение всего процесса опорожнения коэффициент сопротивления трения λ = 0,025.
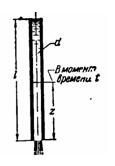
Скачать решение задачи 12-8 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-9. Определить время полного опорожнения трубы с момента открытия ее нижнего конца, если ее длина l = 10 м и угол наклона к горизонту α = 45°. Гидравлическим сопротивлением трубы пренебрегать.
Отвзт. T0 = 1,7 с.
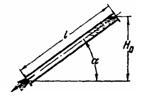
Скачать решение задачи 12-9 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-10. Жидкость, находящаяся в изогнутой трубке, выведена из начального положения равновесия так, что ее свободная поверхность сместилась на величину z0 (начальная амплитуда), совершает затем колебания около этого положения.
Определить период колебания столба жидкости (предполагая, что трение отсутствует). при l = 0,5 м и φ = 45°.
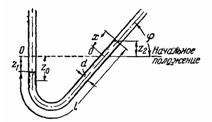
Скачать решение задачи 12-10 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-11. Заполняющая U-образную трубку жидкость, будучи выведена из положения равновесия (начальная амплитуда z0 = 10 см), совершает затем колебательное движение.
Определить период колебания, а также амплитуду z' в конце первого периода, если диаметр трубки d = 1 см, длина жидкого столба l = 60 см и китематическая вязкость жидкости v = 0,1 Ст. Режим движения жидкости в трубке считать ламинарным.
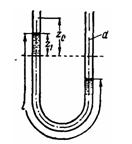
Скачать решение задачи 12-11 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12-12. Жидкость, заполняющая два соединенных между собой резервуара, будучи выведена из положения равновесия, начинает совершать свободные колебания около этого положения. Пренебрегая сопротивлением, определить период колебания жидкости, если резервуары имеют поперечные сечения F1 и F2 и соединены трубой, длина которой l, а площадь поперечного сечения f во много раз меньше площади каждого из резервуаров. Указание. Воспользоваться уравнением (12-7) и пренебречь членом, содержащим
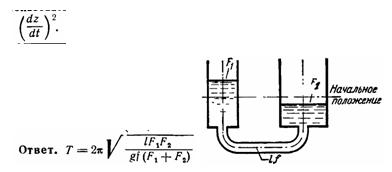
Задача (Куколевский И.И.) 12-13. К паровому котлу с площадью зеркала F1 подключено водомерное стекло с площадью поперечного сечения F2. Соединительная трубка длиной l имеет площадь поперечного сечения f.
Жидкость в паровом котле выведена из состояния покоя и ее зеркало совершает свободные колебания. Пренебрегая сопротивлениями и считая амплитуду колебаний малой, определить период колебания жидкости в водомерном стекле, если h = 0,1 м, f = 1 см2, F2 = 2 см2 и L = 0,25 м.

Задача (Куколевский И.И.) 12-14. Предохранительный клапан, пропуская расход жидкости, находится в потоке жидкости в равновесии на расстоянии у = 5мм от седла. Масса клапана m = 0,5 кг.
Пренебрегая сжимаемостью жидкости, составить дифференциальное уравнение колебаний выведенного из положения равновесия клапана и определить частоту его колебаний выведенного из положения равновесия клапана и определить частоту его колебаний, считая, что сила трения R действующая на клапан, линейно зависит от скорости: R = Θ*u(t) где Θ - коэффициент демпфирования, Θ = 2,5 Н*с/см, u(t) - переменная во времени скорость колеблющегося клапан.
Жесткость пружины С = 20 Н/см; начальное поджатие пружины при закрытом клапане y0 = 50мм. Массой пружины пренебречь

Скачать решение задачи 12-14 (Куколевский И.И.) (цена 100р)
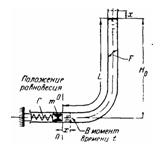
Задача (Куколевский И.И.) 12-15 Система, состоящая из пружины, поршня и жидкого столба длиной L, выведена из состояния покоя и затем совершает свободные колебания.
Определить закон движения жидкости и вычислить период колебания, если масса поршня m и площадь поперечного сечения трубки F. Режим течения считать ламинарным; плотность и вязкость жидкости р и v. Сравнить с периодом колебаний, вычисленным в предположении отсутствия трения.
Скачать решение задачи 12-15 (Куколевский И.И.) (цена 100р)
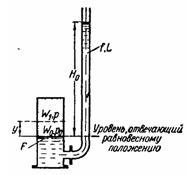
Задача (Куколевский И.И.) 12-16. Жидкость в трубе, подключенной к воздушному колпаку поршневого насоса, выведена из положения равновесия. Пренебрегая сопротивлением, определить частоту собственных колебаний жидкости, если длина трубы, заполненной жидкостью, L, площадь ее поперечного сечения f, площадь сечения колпака равна F и объем воздуха в колпаке при равновесном положении уровней равен W0.
Высота столба жидкости, соответствующая давлению в колпаке в положении равновесия, равна Н0 Инерцией жидкости в колпаке пренебречь, считая площадь поперечного сечения колпака значительно большей, чем площадь поперечного сечения трубы.
Скачать решение задачи 12-16 (Куколевский И.И.) (цена 100р)
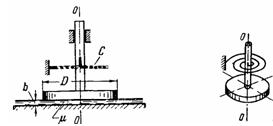
Задача (Куколевский И.И.) 12-17. Круглый диск (D = 150 мм), к. которому в его плоскости приложена и внезапно удалена пара сил, совершает крутильные колебания относительно оси О-О. Затухание колебаний происходит благодаря трению в вязком слое жидкости по торцу диска.
Пренебрегая массой стержня, определить частоту крутильных колебаний, если масса диска m = 1 кг, динамическая вязкость жидкости μ = 1 П и толщина жидкого слоя b = 0,5 мм. Жесткость пружины С = 0,1 Н*м/рад. Течение в вязком слое считать ламинарным.
Скачать решение задачи 12-17 (Куколевский И.И.) (цена 100р)
Часть 12-2 Неустановившееся движение жидкости
Задача (Куколевский И.И.) 12.18. Затвор, установленный на конце трубопровода (L = 100 м; D = 100 мм), работающего под напором воды H0 = 10м, уменьшает расход от его начального значения Q0 = 10 л/с до нуля за время Т3 = 1 с. Принимая закон закрытия затвора линейным и считая трубопровод и жидкость неупругими, определить максимальное повышение давления в трубопроводе в процессе закрытия. Потерями напора в трубопроводе пренебречь.
Ответ. ΔPин=0,24 МПа.
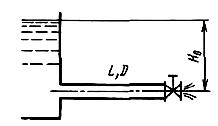
Задача (Куколевский И.И.) 12.19. Затвор, установленный в конце трубопровода, состоящего из двух участков (L1 = 50 м; D1 = 100 мм и L2 = 50 м; D2 = 120 мм), закрываясь по линейному закону, уменьшает расход воды от Q0 = 15 л/с до Q1 = 5 л/с в течение T3 = 1 с. Располагаемый напор H0 = 40 м.
Определить максимальное повышение давления в трубопроводе в процессе закрытия, считая его стенки и жидкость неупругими и пренебрегая потерями напора.
Ответ. ΔPин =0,15 МПа.
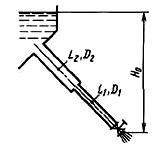
Задача (Куколевский И.И.) 12.20. Трубопровод, имеющий общую длину l = 20 м и внутренний диаметр d = 50 мм и подключенный к баку с водой под напором H0 = 4 м, мгновенно закрывается.
Определить скорость а распространения ударной волны и ударное повышение давления ΔPуд, если толщина стенок трубы δ = 6 мм и материал ее - сталь (Е = 2*105 МПа). Модуль упругости воды K = 2000 МПа.
Как изменится ударное давление, если стальная труба будет заменена чугунной (Е = 0,9*105 МПа) тех же размеров? Коэффициент сопротивления трения принять λ = 0,03.
Ответ. Для стальной трубы а = 1365 м/с и ΔPуд = 3,5 МПа.
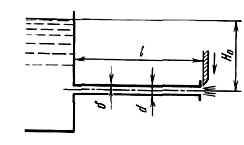
Задача (Куколевский И.И.) 12.21. Центробежный насос подает воду на высоту H0 = 16 м по трубопроводу, имеющему общую длину l = 105 м и внутренний диаметр d = 75 мм.
Внезапно двигатель насоса отключается от сети. Некоторое время столб воды в трубопроводе продолжает двигаться за счет инерции в прежнем направлении, затем скорость движения уменьшается до нуля, после чего движение жидкости происходит в обратном направлении под действием напора Н0. В этот момент происходит закрытие обратного клапана, установленного в нижнем конце трубы, и возникает гидравлический удар. Определить ударное повышение давления, если обратный клапан закрылся через Т = 1 с после начала движения жидкости в обратном направлении. При движении жидкости через насос последний следует рассматривать как местное сопротивление с коэффициентом сопротивления ζ = 10 (отнесенным к скорости в трубопроводе), Коэффициент сопротивления задвижки ζ3 = 4, коэффициент трения в трубе принять λ = 0,025. Для обратного клапана, проходное сечение которого равно площади сечения трубы, Cк = 2. Толщина стенок трубы б=4 мм, материал ее - сталь (Е = 2•105 МПа). Модуль упругости воды К = 1000 МПа.
Ответ ΔPуд = 1.75 МПа.
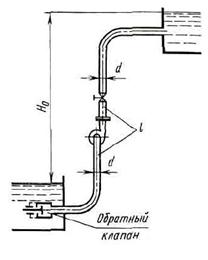
Задача (Куколевский И.И.) 12.22. Смазка параллелей ползуна производится из масленки самотеком по трубке диаметром d = 6 мм и длиной l = 1м через отверстие, периодически открываемое ползуном.
Считая трубку и жидкость неупругими, определить количество поступающего из масленки смазочного масла за один оборот коленчатого вала, если отверстие остается при этом открытым в течение Т= 1 с.
Кинематическая вязкость масла v = 0,5 Ст. Напор Н0 = 0,8 м. Течение жидкости считать ламинарным, пренебрегая кинетической энергией выхода из трубки.

Задача (Куколевский И.И.) 12.23. На конце трубы мгновенно открывается кран А. Найти минимальное давление перед ним, если коэффициент расхода открытого крана μ0 = 0,6, скорость ударной волны а = 1000 м/с, статический напор перед закрытым краном h0 = 100 м. Исследовать закон изменения расхода через кран. Трением в трубе пренебречь.
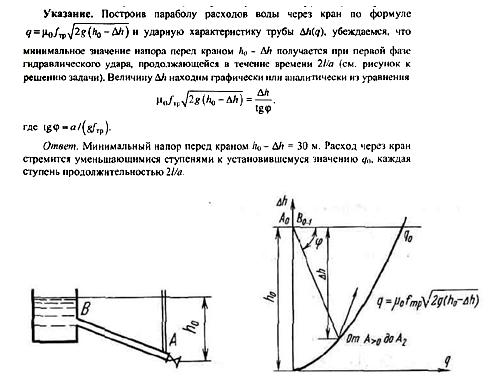
Скачать решение задачи 12-23 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12.24. В трубопроводе длиной l = 100 м и диаметром d = 100 мм, на конце которого установлен затвор, движется вода со скоростью v0 = 2 м/с.
Построить график зависимости максимального ударного повышения напора в трубопроводе от времени полного закрытия затвора. Считать, что принятый закон закрытия дает линейное уменьшение скорости потока перед затвором по времени. Потерями напора в трубопроводе пренебречь. Построения выполнить, учитывая упругость системы (скорость ударной волны а = 1000 м/с) и считая систему неупругой. Для этил случаев сравнить ударное повышение напора при времени полного закрытия Т3 = 2*l/а. Указание. При непрямом ударе и линейном законе уменьшения скорости
Задача (Куколевский И.И.) 12.25. На конце трубы длиной l по направлению к резервуару трогается из неподвижного положения поршень с постоянным ускорением j. Найти максимальное и минимальное ударные давления перед поршнем и сравнить с результатом, полученным для неупругой системы жидкость - трубопровод.
Ответ. Δh=2*l*j/g т.е в два раза больше, чем для неупругой системы; Δhmin=0.
Задача (Куколевский И.И.) 12.26. Тупиковая труба заполнена жидкостью под атмосферным давлением. Кран В мгновенно открывается, сообщая трубу с резервуаром под постоянным напором h0. Определить амплитуду колебаний давления у тупика в сечении А.
Ответ. Δhmax =2*h0; hmin = 0.
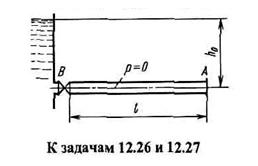
Задача (Куколевский И.И.) 12.27. Для условий предыдущей задачи найти давление в середине трубы в момент 3*l/a (l - длина трубы, а - скорость ударной волны). Указание. Для решения задачи использовать двух подвижных наблюдателей, выбывающих из сечений А л В навстречу друг другу так, чтобы встреча их произошла в середине трубы в момент 3*l/a. Искомый режим определяется пересечением прямых, выходящих из точек А25 и В25.
Ответ. Напор равен h0.
Задача (Куколевский И.И.) 12.28. На конце трубы совершает гармонические кояе-бания поршень, так что вытесняемый им расход изменяется по закону q=qmax*sinw*t, где w - круговая частота колебаний. Показать, что при w = π*a*l/(2*l), где l - длина трубы и a - скорость ударной волны, имеет место резонанс, т.е. давление перед поршнем при отсутствии трения неограниченно возрастает. Смешения поршня считать малыми по сравнению с длиной трубы. Указание. Воспользоваться методикой, примененной при решении примера 2 во введении.
Задача (Куколевский И.И.) 12.29. На конце трубы, присоединенной к резервуару большой емкости, установлен кран, открытый настолько, что его коэффициент расхода μ0 = 0,48. Напор перед краном h0 = 50 м, длина трубы l = 160 м, диаметр d = 100 мм, скорость ударной волны а = 770 м/с. Производится мгновенное частичное закрытие крана, при котором новое значение коэффициента расхода μ1 = 0,016. Определить максимальное значение ударного напора Δhуд и построить зависимость расхода через кран и напора перед ним по времени.
Ответ. Δhуд = 60 м.
Задача (Куколевский И.И.) 12.30. К насосу подключен горизонтальный трубопровод длиной l = 12м, диаметром d = 125 мм с краном на конце. Кран частично открыт так, что его коэффициент расхода μ = 0,031. При включении насоса его подача нарастает по прямой от нуля до q0 = 10 л/с за время l = 0,05 с. Скорость ударной волны а = 1200 м/с, Определить закон изменения давления у насоса (сечение А) по времени. Трением в трубе пренебречь.
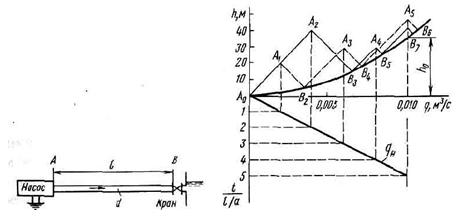
Скачать решение задачи 12-30 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 12.31. Каким будет максимальный ударный напор в сечении А у насоса в предыдущей задаче, если принять, что расход насоса qн возрастает мгновенно от нуля до 0,010 м3/с и остается в последующем постоянным. Найти максимальный расход жидкости через кран. Трением в трубе пренебречь.
Ответ. ha = 100 м и сохраняется постоянным на отрезке времени от 0 до 0,02 с; qmax = 0,0135 м!/си сохраняется постоянным на отрезке времени от 0,01 до 0,03 с.
Задача (Куколевский И.И.) 12.32. Труба длиной l = 400 м и диаметром d = 110 мм с соплом dс = 63 мм на конце заполнена водой. Напор h0 = 90 м, коэффициент расхода сопла μ = 0,98, скорость ударной волны в трубе а = 1390 м/с. В сечении А производится неполное мгновенное открытие заслонки, так что ее коэффициент расхода сопла μ = 0,322. Найти графическим путем закон изменения расхода через сопло qc по времени. Указать установившееся значение qуст расхода, к которому стремится qс. Трением в трубе скоростным напором в ней пренебречь.
Указание. Параболу потерь напора в заслонке откладывать на графике от уровня h0 вниз, а параболу напора в сечении В перед соплом вверх от линии Н = 0 (от оси расходов).
Ответ.
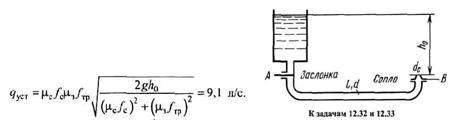
Задача (Куколевский И.И.) 12.33. В условиях предыдущей задачи произведено мгновенное полное открытие заслонки А. При каком отношении площадей сопла и трубы fc/fтр максимальная величина напора в сечении В перед соплом составит: 1) h0; 2) 1,5h0 3) 2h0? Каковы будут при этом установившиеся значения расхода через сопло qуст? Трением в трубе пренебречь. Указание. Построив схематический чертеж графического решения, вычислить требуемые величины аналитически. Ответ.
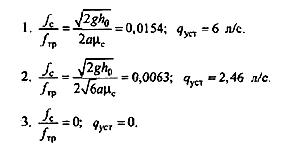
Задача (Куколевский И.И.) 12.34. На конце трубы, заполненной водой, находится а неподвижном состоянии поршень. Начальное избыточное давление в трубе равно нулю. Масса m, движущаяся со скоростью v0, ударяет в шток поршня, после чего поршень и масса m движутся как одно тело. Вследствие большой длины трубы и вязкости жидкости отраженные волны не доходят до поршня. Определить закон изменения давления перед поршнем и закон движения поршня в функции времени. Трением поршня о стенки трубы и его массой пренебречь. Скорость ударной волны в трубе равна а. Указание. Воспользоваться формулой Жуковского в дифференциальной