Часть 11-1 Истечение под переменным напором
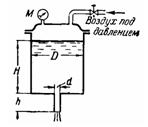
Задача (Куколевский И.И.) 11-1. Какое давление M воздуха нужно поддерживать в баке, чтобы его опорожнение происходило в два раза быстрее, чем при атмосферном давлении над уровнем воды, каково будет при этом время Т опорожнения бака?
Диаметр бака D = 800 мм, его начальное заполнение Н = 900 мм. Истечение происходит через цилиндрический насадок диаметром d = 25 мм и высотой h = 100мм, коэффициент расхода которого μ = 0,82.
Ответ. М = 11,85 кПа; Т = 3 мин 13 сек.
Скачать решение задачи 11-1 (Куколевский И.И.) (цена 100р)
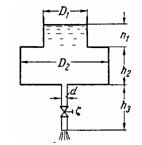
Задача (Куколевский И.И.) 11-2. Определить время опорожнения составного цилиндрического резервуара (D1 = 1,5 м; D2 = 2,2 м; h1 = 1 м, h2 = 1,5 м) через вертикальную трубу высотой h3 = 2 м и диаметром d = 60 мм при открытом вентиле с коэффициентом сопротивления ξ = 4. Коэффициент сопротивления трения в трубе принять равным λ = 0,03.
Ответ. T = 14,2 мин.
Скачать решение задачи 11-2 (Куколевский И.И.) (цена 100р)
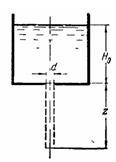
Задача (Куколевский И.И.) 11-3. Определить высоту сливной трубы г, при которой опорожнение цилиндрического бака будет происходить в два раза быстрее, чем через отверстие такого же диаметра. Начальное заполнение бака H0 = 4 м, диаметр отверстия d= 60 мм, его коэффициент расхода μ = 0,6. Коэффициент сопротивления трения в трубе принять λ = 0,03.
Ответ, z = 1,36 м.
Скачать решение задачи 11-3 (Куколевский И.И.) (цена 100р)
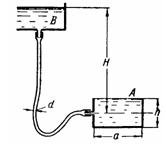
Задача (Куколевский И.И.) 11-4. Призматический бак А со стороной квадратного основания а = 2 м и высотой h =1,6 м заполняется бензином из центрального бензохранилища В, уровень в котором постоянен (Н = 5 м). Заполнение происходит через гибкий шланг длиной l = 7 м, выходное сечение которого находится на середине высоты бака. Определить диаметр шланга d, при котором бак будет заполняться в заданное время Т = 15 мин, приняв коэффициент сопротивления трения в шланге равным λ = 0,05; местными потерями в шланге пренебречь.
Ответ. d = 53 мм.
Скачать решение задачи 11-4 (Куколевский И.И.) (цена 100р)
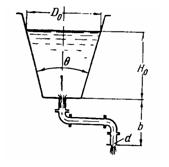
Задача (Куколевский И.И.) 11-5. Определить время опорожнения конического сосуда (θ = 30°), если опорожнение происходит через трубу, диаметр которой d = 15 мм и суммарный коэффициент сопротивления ξ = 2,5. Начальный уровень жидкости H0 = 0,85 м; D0 = 1 м; вертикальное расстояние от выходного отверстия трубы до дна сосуда b = 0,6 м.
Ответ. Т = 21 мин 50 с.
Скачать решение задачи 11-5 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-6. Из емкости, имеющей постоянное по высоте сечение, площадью F = 20 м2 жидкость откачивается насосом с постоянным расходом QН = 4 л/сек, а также вытекает в атмосферу по горизонтальной трубе диаметром d = 50 мм, суммарный коэффициент сопротивления которой ξ = 5. Определить время понижения уровня на величину а = 1 м.
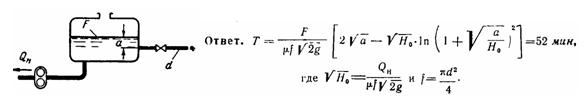
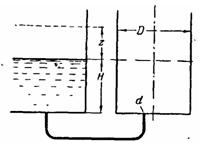
Задача (Куколевский И.И.) 11-7. Бак диаметром D = 600 мм заполняется водой из резервуара с неизменным уровнем H = 1,2 м. Заполнение происходит через трубу диаметром d = 25 мм, суммарный коэффициент сопротивления которой равен ξ = 8.
1 Определить время заполнения бака до уровня в резервуаре.
2 На какую высоту z следует поднять уровень в резервуаре, чтобы заполнение бака на ту же высоту Н происходило в два раза быстрее
Ответ. Т = 14,25 мин; z = 9Н/16.
Скачать решение задачи 11-7 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-8. Определить время опорожнения целиком заполненного шарового сосуда радиусом R = 0,8 через отверстие, диаметр которого d0 = 50 мм (коэффициент расхода μ = 0,62). Давление на свободной поверхности жидкости во время опорожнения считать атмосферным. За какое время из сосуда вытечет половина содержащегося в нем объема воды?
Ответ. время половинного опорожнения T2 = 200 с.
Время полного опорожнения
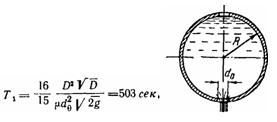
Скачать решение задачи 11-8 (Куколевский И.И.) (цена 100р)
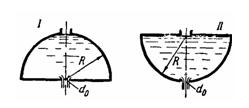
Задача (Куколевский И.И.) 11-9. Сравнить время опорожнения полушарового сосуда, расположенного сферой вверх (I) со временем опорожнения полушарового сосуда того же радиуса R, располюженного сферой вниз (II). В обоих случаях истечение происходит через одинаковое отверстие d0. Давление на свободной поверхности жидкости при истечении считать атмосферным.
Ответ T(I)/T(II)=12/7
Скачать решение задачи 11-9 (Куколевский И.И.) (цена 100р)
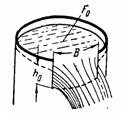
Задача (Куколевский И.И.) 11-10. Определить, за какое время из резервуара площадью F0 = 300 м2 через прямоугольный вырез, в боковой стенке шириной B=1,6 м выльется объем воды W = 330 м3, если начальный уровень воды над порогом равен h0 = 1,2 м. Коэффициент расхода водослива принять m = 0,4.
Ответ. Т = 7,9 мин.
Скачать решение задачи 11-10 (Куколевский И.И.) (цена 100р)
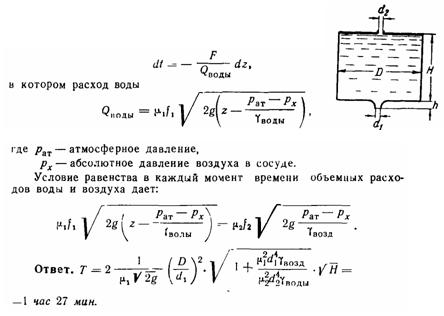
Задача (Куколевский И.И.) 11-11. Определить время опорожнения целиком заполненного цилиндрического сосуда через сходящееся сопло (d1 =25 мм; μ1 = 0,97), если в верхней крышке сосуда имеется отверстие (d2 = 3 мм, μ2 = 0,6), через которое засасывается воздух по мере вытекания воды. Диаметр сосуда D = 1,2 м, его высота H= 1,5 м, плотность воздуха ρвозд = 1,2 кг/м3.
Задачу решать, исходя из равенства объемных расходов воды и воздуха, пренебрегая сжимаемостью послед него. Высотой сопла Н пренебречь.
Указание. Дифференциальное уравнение процесса истечения
Скачать решение задачи 11-11 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-12. Сосуд с переменным по высоте сечением опоражнивается через донный сходящийся насадок.
1) Какоq должна быть зависимость радиуса сосуда R от высоты сечения z над насадком, чтобы опускание уровня жидкости происходило равномерно?
2) Определить диаметр d насадка, при котором постоянная скорость опускания уровня при опорожнении сосуда такой формы будет равняться v = 1 мм/с, если начальные значения радиуса и заполнения сосуда равны R0 = 125мм и z0 = 310 мм. Коэффициент расхода насадка принимать постоянным и равным μ = 0,95.
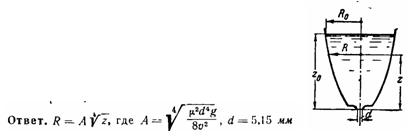
Скачать решение задачи 11-12 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-13. Открытая цистерна диаметром D = 2,4 м и длиной L = 6 м, целиком заполненная бензином, опоражнивается через сливную трубу, диаметр и длина которой равны d = 50 мм и l = 7 м, а выходное сечение находится на уровне нижней точки сечения цистерны. Суммарный коэффициент местных сопротивлений в трубе ξ = 8, коэффициент сопротивления трения принять 0,025.Определить время опорожнения цистерны.
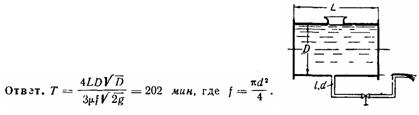
Скачать решение задачи 11-13 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-14. Определить время опорожнения цилиндрического резервуара, диаметр которого D = 0,8 м, через два круглых отверстия каждое диаметром d0 = 10 мм, расположенные на расстоянии а = 0,5 м по высоте друг от друга. Начальное положение уровня H0 = 1,5 м. Коэффициент расхода каждого из отверстий μ = 0,62.
Ответ. Т = 1 ч 22 мин
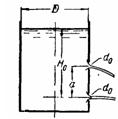
Скачать решение задачи 11-14 (Куколевский И.И.) (цена 100р)
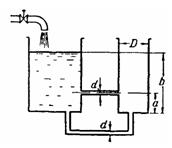
Задача (Куколевский И.И.) 11-15. Бак диаметром D = 600 мм заполняется водой из резервуара с постоянным уровнем b = 1,5 м через две короткие трубы одинакового диаметра d = 25 мм. Одна из труб примыкает к дну бака, другая - к его боковой стенке на высоте а = 0,6 м от дна.
Определить время заполнения бака до уровня в резервуаре, учитывая в трубах только местные потери (коэффициент сопротивления каждого из колен ξ =1,2; коэффициент сопротивления входа ξ = 0,5).
Ответ. T = 282 с.
Скачать решение задачи 11-15 (Куколевский И.И.) (цена 100р)
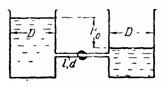
Задача (Куколевский И.И.) 11-16. Определить время выравнивания уровней в двух резервуарах при начальном напоре H0 = 4 м. Диаметры резервуаров равны D1 = 1,6 м и D2 = 3,2 м; h0 = 1,5 м. Перетекание происходит через цилиндрический насадок диаметром d=100 мм с коэффициентом расхода μ = 0,82.
Ответ. T = 9,08 мин
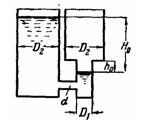
Скачать решение задачи 11-16 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-17. Два резервуара с одинаковыми диаметрами D = 0,8 м, заполненные маслом (v = 1,4 Ст) с начальной разностью уровней H0 = 1,2 м, соединены трубкой диаметром d = 12 мм и длиной l = 6 м.
Найти время, потребное для того, чтобы разность уровней уменьшилась до H = 0,1 м, учитывая в трубке только потери трения. Указание. Предварительно выяснить режим течения в трубке (см. введение гл. 9).
Ответ. Т = 2,36 ч.
Скачать решение задачи 11-17 (Куколевский И.И.) (цена 100р)
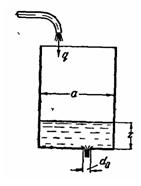
Задача (Куколевский И.И.) 11-18. В первоначально пустой бак квадратного сечения (а = 800 мм) подается постоянное количество воды q = 2 л/с. Одновременно происходит вытекание поступающей воды через донное отверстие диаметром d0 = 30 мм (коэффициент расхода отверстия μ = 0,6).
1) Каков предельный уровень zmax отвечающий установившейся работе системы.
2) Какое время требуется для того, чтобы разность между zmax и текущим уровнем z стала равной Δz = 0,1 м?
Ответ. 1) zmax = 1,1 м. 2) t = 24,2 мин.
Скачать решение задачи 11-18 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-19. Шлюзовая камера заполняется из водохранилища с неизменным уровнем путем подъема ворот на высоту S = 2 м, производимого с постоянной скоростью v = 10 мм/с в течение всего времени заполнения камеры.
1 Определить высоту H1, на которую поднимается уровень воды в камере за время подъема ворот, а также время полного заполнения камеры, если длина камеры L = 180 м и начальная разность уровней H0 = 10 м.
2 Какова должна быть скорость подъема ворот, чтобы камера заполнилась целиком к моменту их подъема на заданную высоту S?
Коэффициент расхода отверстия под нижней кромкой ворот считать постоянным и равным μ = 0,6.
Указание. Для первого этапа заполнения камеры (во время подъема ворот) дифференциальное уравнение процесса имеет вид:
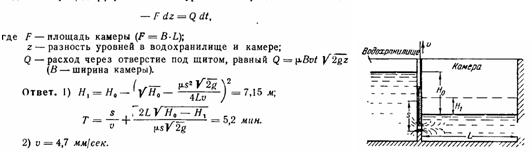
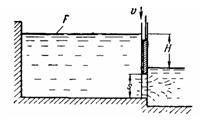
Задача (Куколевский И.И.) 11-20. Шит А, опускаясь с постоянной скоростью v = 0,05 м/сек, перекрывает квадратно отверстие (а = 1 м) в вертикальной стенке. Считая уровень воды постоянным (Н = 3 м), определить, сколько воды вытечет за время закрытия отверстия. Коэффициент расхода отверстия принять в процессе закрытия постоянным и равным μ = 0,59.

Задача (Куколевский И.И.) 11-21. Шлюзовая камера площадью F = 800 м2 имеет перепускное прямоугольное отверстие высотой s = 2 м и шириной B = 4 м, которое начинает закрываться щитом, движущимся с постоянной скоростью v = 0,05 м/с.
Определить понижение у уровня в шлюзовой камере за время закрытия отверстия, истечение через которое происходит под постоянный уровень. Начальный напор H= 5 м. Коэффициент расхода отверстия принять постоянным и равным μ = 0,65.
Ответ, у = 1,2 м.
Скачать решение задачи 11-21 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 11-22. Квадратный ящик со стороной основания а = 3 м, высотой h = 1,2 м и толщиной стенок б = 150 мм плавает, погруженный в воду на глубину h0 = 0,6 м. Определить время затопления ящика с момента открытия донного отверстия диаметром d = 30 мм, (коэффициент расхода μ = 0,82).
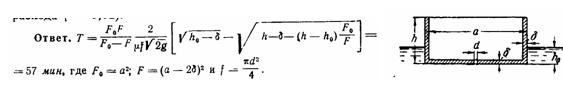
Задача (Куколевский И.И.) 11-23. Определить время затопления тонкостенного сосуда после открытия донного отверстия диаметром d0 = 25 мм. Сосуд имеет два цилиндрических участка, диаметры которых D1 = 1,2 м и D2 = 0,6 м, а высоты h1 = 0,8 м и h2 = 0,5 м. Начальное погружение сосуда h0 = 0,85 м. Коэффициент расхода отверстия принять μ = 0,6.
Указание. Затопление сосуда происходит в два этапа:
1) погружение при переменном напоре истечения через отверстие до момента времени, когда сосуд заполнится водой на высоту h2
2) погружение при постоянном напоре истечения равном z=

Скачать решение задачи 11-23 (Куколевский И.И.) (цена 100р)


